К оглавлению

Триангуляция Делоне

С.И.Хашин

1. Определения

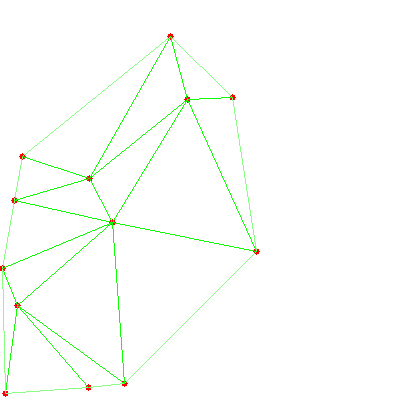
Определение. Триангуляцией называется планарный граф, все внутренние области которого являются треугольниками.

Определение. Триангуляция называется оптимальной, если сумма длин всех рёбер минимальна среди всех возможных триангуляций, построенных на тех же исходных точках.

Для большинства реальных задач существующие алгоритмы построения оптимальной триангуляции неприемлемы ввиду слишком высокой трудоёмкости. При необходимости на практике применяют приближенные алгоритмы, например «жадный» алгоритм построения триангуляции или триангуляцию Делоне.

1.1.Жадный алгоритм триангуляции

Шаг 1. Генерируется список всех возможных отрезков, соединяющих пары исходных точек, и он сортируется по длинам отрезков.

Шаг 2. Начиная с самого короткого, последовательно выполняется вставка отрезков в триангуляцию. Если отрезок не пересекается с другими ранее вставленными отрезками, то он вставляется, иначе он отбрасывается.

Заметим, что если все возможные отрезки имеют разную длину, то результат работы этого алгоритма однозначен, иначе он зависит от порядка вставки отрезков одинаковой длины.

Трудоемкость работы жадного алгоритма при некоторых его улучшениях составляет ~O(N²logN) [3]. В связи со столь большой трудоемкостью на практике он почти не применяется.

1.2. Триангуляция Делоне

Пусть на плоскости дан набор точек {P_i=(x_i,y_i)}. Триангуляцией Делоне называется такое разбиение плоскости на треугольники с вершинами в заданных точках, что ни одна окружность, описанная вокруг любого из треугольников, не содержит других точек из разбиения.

Другое определение триангуляции Делоне дают два следующих определения.

Определение. Говорят, что пара соседних треугольников триангуляции удовлетворяет условию Делоне, если этому условию удовлетворяет триангуляция, составленная только из этих двух треугольников.

Определение. Говорят, что треугольник триангуляции удовлетворяет условию Делоне, если этому условию удовлетворяет триангуляция, составленная только из этого треугольника и трёх его соседей (если они существуют).

Триангуляция Делоне всегда существует. Чаще всего она единственная, но в некоторых случаях (см.ниже) таких триангуляций существует несколько.

Многие алгоритмы построения триангуляции Делоне используют следующую теорему:

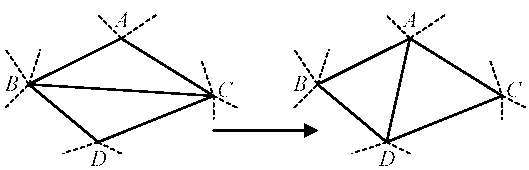
Теорема 1. Триангуляцию Делоне можно получить из любой другой триангуляции по той же системе точек, последовательно перестраивая пары соседних треугольников (ABC) и (BCD), не удовлетворяющих условию Делоне, в пары треугольников (ABD) и (ACD) (см.рис.). Такая операция перестроения также часто называется флипом (flip).

Теорема 2. Триангуляция Делоне обладает максимальной суммой минимальных углов всех своих треугольников среди всех возможных триангуляций.

Теорема 3. Триангуляция Делоне обладает минимальной суммой радиусов окружностей, описанных около треугольников, среди всех возможных триангуляций.

2. Методы построения триангуляции Делоне

В настоящее время известно значительное количество различных алгоритмов построения триангуляции Делоне. Их можно разделить на следующие группы:

• Итеративные алгоритмы
• Алгоритмы слияния
• Алгоритмы прямого построения
• Двухпроходные алгоритмы.

2.1. Итеративные алгоритмы

Все итеративные алгоритмы имеют в своей основе очень простую идею последовательного добавления точек в частично построенную триангуляцию Делоне. Формально это выглядит так.

Итеративный алгоритм построения триангуляции Делоне.

Дано множество из N точек.

• Шаг 1. На первых трех исходных точках строим один треугольник.
• Шаг 2. В цикле по n для всех остальных точек выполняем шаги 3–5.
• Шаг 3. Очередная n-я точка добавляется в уже построенную структуру триангуляции следующим образом. Вначале производится локализация точки, т.е. находится треугольник (построенный ранее), в который попадает очередная точка. Либо, если точка не попадает внутрь триангуляции, находится треугольник на границе триангуляции, ближайший к очередной точке.
• Шаг 4. Если точка попала на ранее вставленный узел триангуляции, то такая точка обычно отбрасывается, иначе точка вставляется в триангуляцию в виде нового узла. При этом если точка попала на некоторое ребро, то оно разбивается на два новых, а оба смежных с ребром треугольника также делятся на два меньших. Если точка попала строго внутрь какого-нибудь треугольника, он разбивается на три новых. Если точка попала вне триангуляции, то строится один или более треугольников.
• Шаг 5. Проводятся локальные проверки вновь полученных треугольников на соответствие условию Делоне и выполняются необходимые перестроения.
• Конец алгоритма.

Различные версии этого алгоритма различаются способом выбора очередной точки и методом локализации, последовательностью перестроений.

2.2. Алгоритмы триангуляции Делоне слиянием

В целом, все алгоритмы слияния предполагают разбиение исходного множества точек на несколько подмножеств, построение триангуляций на этих подмножествах, а затем объединение (слияние) нескольких триангуляций в одно целое.

Например, множество точек разбивается на две как можно более равные части с помощью горизонтальных и вертикальных линий. Алгоритм триангуляции рекурсивно применяется к подчастям, а затем производится слияние (объединение, склеивание) полученных подтриангуляций.

В других вариантах триангуляции разбиение на части производится путем выбора диаметра – самого длинного отрезка между данными точками, путем разбиения точек на горизонтальные и/или вертикальные полосы и т.д.

2.3. Алгоритмы прямого построения

(Алгоритм такого типа а у нас и используется в настоящее время)

Во всех вариантах этого алгоритма мы начинаем с некоторого начального (базового) отрезка, расположенного на границе. Далее для него необходимо найти соседа Делоне – узел, который вместе с концами данного базового отрезка в триангуляции Делоне является вершинами одного треугольника. Процесс поиска можно представить как рост «пузыря» от базового отрезка, пока не встретится какой-нибудь узел. «Пузырь» – это окружность, проходящая через точки A и B, и центр которой находится на срединном перпендикуляре к базовому отрезку.

В пошаговом алгоритме для поиска соседа Делоне нужно выбрать среди всех точек P_i триангуляции такую, что угол AP_iB будет максимальным. Найденный сосед Делоне соединяется отрезками с концами базовой линии и образует треугольник AP_iB. Новые рёбра AP_i и BP_i построенного треугольника помечаются как новые базовые отрезки, и процесс поиска треугольников продолжается.

Трудоемкость пошагового алгоритма составляет ~O(N²) в среднем и в худшем случае.

Цитата из книги [1]: «Из-за столь большой трудоемкости на практике такой алгоритм почти не применяется». Но мы как раз его и используем. В основном из-за того, что этот алгоритм несколько проще в реализации. Кроме того, при количестве точек ~100-500 алгоритм все-таки работает достаточно быстро.

2.4. Двухпроходные алгоритмы

При построении триангуляции Делоне итеративными алгоритмами и алгоритмами слияния для каждого нового треугольника должно быть проверено условие Делоне. Если оно не выполняется, то должны последовать перестроения треугольников и новая серия проверок. На практике довольно большую долю времени отнимают как раз проверки на условие Делоне и перестроения. Для уменьшения числа проверок условия Делоне и упрощения логики работы алгоритмов можно использовать следующий подход. Вначале за первый проход нужно построить некоторую триангуляцию, игнорируя выполнение условия Делоне. А после этого за второй проход проверить то, что получилось, и провести нужные улучшающие перестроения для приведения триангуляции к условию Делоне.

3. Имеющаяся реализация триангуляции Делоне

3.1. Описание алгоритма

Имеющаяся на сегодняшний день реализация алгоритма триангуляции Делоне, с точки зрения описанной выше классификации, является одной из разновидностей алгоритма «прямого построения триангуляции».

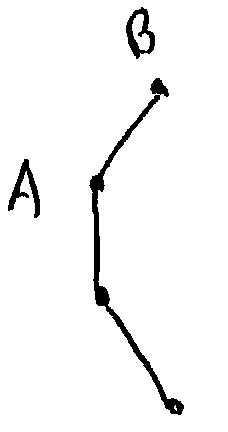
Опишем сначала общую схему алгоритма. В начале найдем первое ребро, которое заведомо должно войти в триангуляцию. Первая его точка (A на рисунке справа) выбирается как точка с наименьшей координатой x (самая левая точка), а среди точек с одинаковой координатой x – как точка с наименьшей координатой y (самая верхняя). Вторая точка начального ребра (B на рисунке) – это точка с наибольшим коэффициентом наклона отрезка [AB].

Список edges – сплошные ребра,

edges_all – сплошные и пунктирные

В процессе работы алгоритма поддерживаются список активных ребер edges. «Активные» ребра – это те, у которых с одной стороны уже есть треугольник, а с другой еще надо пристраивать.

В начале работы он состоит из единственного ребра [AB]. В это список одни ребра добавляются, другие удаляются. Алгоритм заканчивает работу, когда этот список становится пустым.

Дальнейший алгоритм состоит в повторении следующих шагов: выбор очередного ребра из списка edges (и удаление его из списка), и нахождении для него присоединенной вершины – узла, который вместе с концами выбранного ребра в триангуляции Делоне образует вершины одного треугольника. Процесс поиска можно представить как рост «пузыря» от выбранного ребра [AB], пока не встретится какой-нибудь узел. «Пузырь» – это окружность, проходящая через точки A и B, и центр которой находится на срединном перпендикуляре к отрезку.

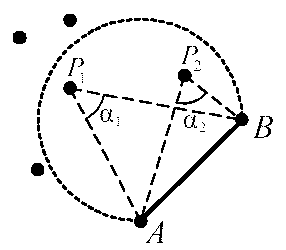
Фактически, мы выбираем среди всех заданных точек P_i такую, что угол AP_iB будет максимальным, или, что то же самое – радиус окружности, проходящей через точки AP_iB будет наименьшим. Найденная присоединенная вершина соединяется отрезками с концами отрезка и образует треугольник AP_iB. Новые рёбра AP_i и BP_i построенного треугольника добавляются в список edges (если их там еще нет), и процесс поиска треугольников продолжается.

При добавлении ребер в список активных, мы вначале проверяем, нет ли там уже этого ребра. Если нет – то просто добавляем. Если уже есть, это означает, что обработка ребра завершена и его надо удалить из списка.

3.2. Тонкое место

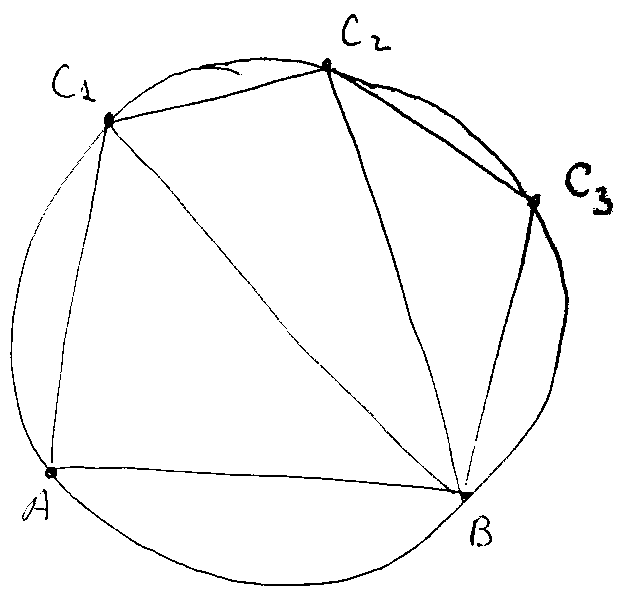
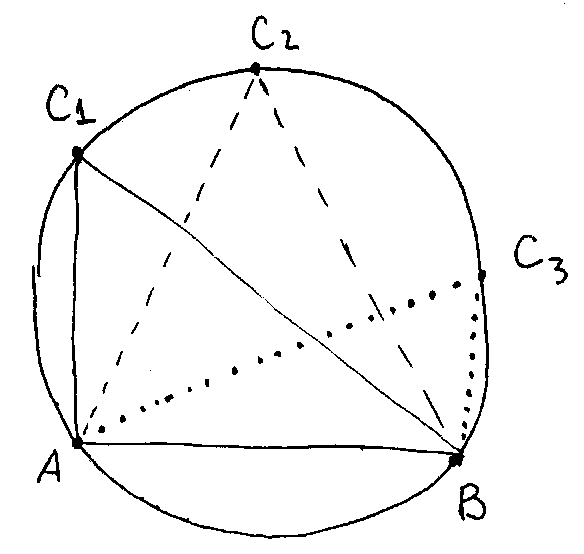
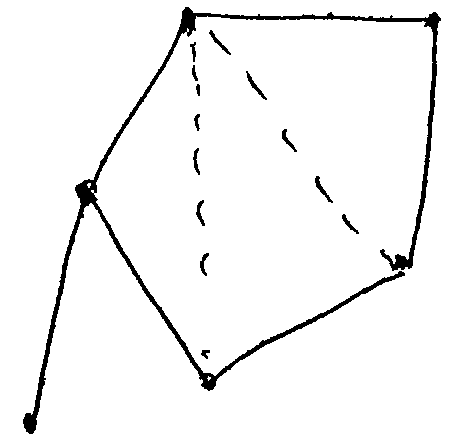
Если точек P с наименьшим радиусом окружности оказывается несколько (рис. слева), надо не выбирать какую-то одну из этих точек, а сразу добавить все получающиеся треугольники и, соответственно, модифицировать список активных ребер. На рисунке справа добавляемые треугольники – это AC₁B, C₁C₂B, C₂C₃B и активные ребра AC₁, C₁C₂, C₂C₃, C₂C₃B.

3.3. Время работы алгоритма

Этот алгоритм для вычисления триангуляции Делоне по набору из n точек выполняется за время О(n²), поскольку при каждой итерации в полный список ребер добавляется ровно одно ребро. Поэтому число итераций равно числу ребер в триангуляции Делоне. Согласно теореме о триангуляции набор точек любая триангуляция содержит не более, чем О(n) ребер, поэтому алгоритм выполняет О(n) итераций. Поскольку на каждую итерацию тратится время О(n), то полностью алгоритм выполняется за время О(n²).

Приведем результаты более точных экспериментов на процессоре Pentium 2.4 Ghz. Так как алгоритм не требует большого объема памяти и не обращается к внешним устройствам, то остальные характеристики компьютера не должны оказывать влияния на скорость работы.

4. Литература

1. Скворцов А.В. Триангуляция Делоне и её применение. Томск. 2002. 128 с.
2. Ruppert J., A Delaunay Refinenent Algorith for Quality 2-Dimensional Mesh Generation. NASA Research Center Journal, 1994-feb.
3. Gilbert P.N. New results on planar triangulations. Tech. Rep. ACT-15, Coord. Sci. Lab., University of Illinois at Urbana, July 1979.

5. Реализация

void Delaunay(pvector &p, pvector &tr); // Триангуляция Делоне: точки p -> треугольники tr

    (tr[0], tr[1], tr[2]) - вершины 0-го треугольника,
    (tr[3], tr[4], tr[5]) - вершины 1-го треугольника,
    ...

// Служебные функции 
void saveTriangles(pvector &triangles, char *filename, char*msg);// записать треугольники в текстовый файл
int  adjoinTriangle(pvector &tr, int k, int r);// Найти соседний треугольник через заданную сторону
void rotateTrangle(pnt *t);             // <*t, *(t+1), *(t+2)> -> <*(t+1), *(t+2), *t>

int     EdgeLen2(pvector &edges, int i);                    // Квадрат длины i-го ребра
void    swapPoints(pnt &p1, pnt &p2);                       // переставить точки
bool    SameP(pnt &v1, pnt &v2);                            // будут ли точки совпадать?
bool    SameE(pnt &v1, pnt &v2, pnt &v3, pnt &v4);          // будут ли отрезки (v1,v2) и (v3,v4) совпадать?
bool    SameT(pnt &v1, pnt &v2, pnt &v3, pnt &w1, pnt &w2, pnt &w3); // проверка равенства треугольников
int     edgeInTri(pvector &tr, pnt &v1, pnt &v2);           // является ли отрезок [v1,v2] стороной какого-то треугольника

#define MAX_TRIANGLE 20 // максимально допустимое количество треугольников, сходящихся к точке

// В массиве it[0..19] вернуть индексы треугольников, входящих в точку p
// В массиве ind[0..19] - индекс точки p среди вершин очередного треугольника (0|1|2)
// возвращаем количество вершин
int getListOfTrianglesInPoint(pvector &tr, pnt &p, int *it, int *ind);

6. Пример работы

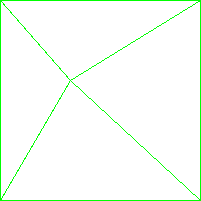
Пример работы:

    pvector p, tr;
    int mx = 201, my = 201;
    p.add(0, 0); p.add(mx - 1, 0);
    p.add(0, my-1); p.add(mx - 1, my - 1);
    p.add(70, 80);
    Delaunay(p, tr);

    int h = 20, N = 10;
    for (int y = 0; y < N; y++)
        for (int x = 0; x < N; x++)
            p.add(x*h, y*h);
    Delaunay(p, tr);

    int mx = 400, my = 400, N=13;
    for (int i = 0; i < N; i++) {
        p.add(1 + hRandom(mx - 2), 1 + hRandom(mx - 2));
    }
    Delaunay(p, tr);

К оглавлению