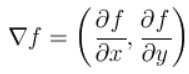
С.И.Хашин
ОГЛАВЛЕНИЕ
Контструктор копирования матрицы запрещен, поэтому передавать матрицу в функцию можно ТОЛЬКО по ссылке. Именно для этого и введен такой запрет.
По умолчанию матрица имеет размеры 0*0, но может быть задан любой размер:
matr a, b(7,8);
Размер матрицы можно в любой момент изменить:
a.setSize(11,12);
b.setSizeClear(7,8);
a.release();
Если новый размер матрицы совпадает с текущим, то никакие действия метод setSize
не выполняет, данные остаются прежними.
Таким образом, "избыточное", "повтороное" применение метода setSize является безопасным
и не приводит к реальным операциям с выделением памяти.
Метод setSizeClear, в отличие от setSize, в любом случае заполняет матрицу нулями.
Этого же (обнуления всех элементов) можно добиться методом clear().
Размеры матрицы можно узнать с помощью методов Mx(), Mx().
Допустимые значения индексов:
0 ≤ x < this->Mx()
0 ≤ y < this->My()
При любом обращении к матрице ВСЕГДА задается сначала x-координата, затем y-координата!
В С++ нельзя обращаться к массиву через две координаты:
int x = a[6,7]; // так нельзя!
Поэтому обращаться приходится через круглые скобки (как в Фортране):
int x = a(6,7); // так можно!
a(3,2) += 7;
Кроме того для обращения к элементам матрицы можно использовать методы:
int get( int x, int y ); // a(x,y)
void put( int x, int y, int value ); // a(x,y) = value;
void inc( int x, int y, int value ); // a(x,y) += value;
Если один из индексов выходит за границы массива вызывается функция обработки ошибки:
void vError(const char *format, ...); // show error function
определённая в модуле vUtil.h.
Для "безопасного" обращения к элементам матрицы имеются два метода:
int safeGet( int x, int y );
void safePut( int x, int y, int value );
Первый метод возвращает элемент наиболее близкий к требуемому:
matr a(4,6); // 0≤ x ≤3, 0≤ y ≤5,
...
int u = a.safeGet(2, 4); // вернёт a(2,4)
int u = a.safeGet(4, 4); // вернёт a(3,4)
int u = a.safeGet(9, 9); // вернёт a(3,5)
int u = a.safeGet(9,-8); // вернёт a(3,0)
Второй метод (safePut) изменит элемент матрицы, если индексы допустимые,
в противном случае ничего не делает.
В любом случае ошибка в этих двух методах никогда не возникает.
Заполнить всю матрицу одним значением позволяет метод
void set( int value );
Заполнить строку или столбец матрицы одним значением:
void fillLine ( int y0, int v ); // заполнить строку значением v
void fillColumn( int x0, int v ); // заполнить столбец значением v
Целое число содержит 4 байта. В компьютерной графике иногда подразумевается, что целое число кодирует RGB-цвет (три младших байта) или RGBA-цвет (все четыре байта). Их можно получить следующими методами:
// RGB, YUV
// Извлекаем из элемента матрицы байты r,g,b,a
int getR( int x, int y ); // младший байт
int getG( int x, int y );
int getB( int x, int y );
int getA( int x, int y ); // стараший байт
Если каждый элемент матрицы содержит в себе RGB-цвет, то мы можем получить из этой матрицы три других, каждая из которых содержит по одной компоненте (числа от 0 до 255):
void toRGB ( matr &r, matr &g, matr &b );
Обратная операция:
void fromRGB( matr &r, matr &g, matr &b );
Помимо пространства RGB в компьютерной графике часто используется цветовое пространство YUV. Для перехода от упакованного представления в три матрицы YUV и обратно применяются методы:
void toYUV ( matr &y, matr &u, matr &v ); // YUV444, ITU-601
void fromYUV( matr &y, matr &u, matr &v ); // YUV444, ITU-601
Записать все элементы матрицы в файл:
void saveText( const char *fname, const char *msg=NULL, char *format = " %5d" );
Например, после выполнения:
matr a(6, 3);
for (int y = 0; y < a.My(); y++)
for (int x = 0; x < a.Mx(); x++)
a(x, y) = x + 10 * y;
a.saveText("a.txt", "Matrix a");
В файле a.txt получим:
6 3 Matrix a
0 1 2 3 4 5
10 11 12 13 14 15
20 21 22 23 24 25
Похожий метод appendText не создает новый файл, а дописывает матрицу в уже существующий. Если такого файла нет, то он создается.
После оператора:
a.saveTextI("a1.txt", "Matrix a", "(%1d,%1d=>%2d), ");
В файле a1.txt получим:
6 3 Matrix a (0,0=> 0), (1,0=> 1), (2,0=> 2), (3,0=> 3), (4,0=> 4), (5,0=> 5), (0,1=>10), (1,1=>11), (2,1=>12), (3,1=>13), (4,1=>14), (5,1=>15), (0,2=>20), (1,2=>21), (2,2=>22), (3,2=>23), (4,2=>24), (5,2=>25),
Такой способ записи удобен, когда размеры матрицы велики (1000*1000) и в сравнительно небольшом окне не экране сложно понять элементы с какими индексами мы сейчас видим.
Обратная операция - чтение матрицы из текстового файла:
void loadText( const char *fname );
В ней предполагается, что файл имеет именно ту структуру, что описана выше,
то есть в первой строке записаны два целых числа: mx и my, размеры матрицы по горизонтали
и по вертикали, всё чте идёт в первой строке после этих чисел рассматривается как комментарий.
Далее в файле должны быть записаны mx*my целых чисел. На самом деле разбиение на
строки полностью игнорируется, числа могут быть разделены пробелами, табуляциями, концами строк.
В матрицу можно прочитать bmp-файл формата bmp-24 без сжатия:
int loadBMP ( const char *fname ); // В каждый элемент упаковываем все три RGB-байта
Функция возвращает код ошибки, поэтому ествественный способ чтения будет:
matr a;
char *fname = "lena.bmp";
int code;
if(code=a.loadBMP(fname)) vError("File %s not open, error code=%d", fname, code);
В таком же виде его можно сохранить (старший байт каждого числа игнорируется):
int saveBMP ( const char *fname ); // В каждом элементе упаковано все три RGB-байта
Матрицу можно сохранить в виде серого bmp-файла:
int saveBMPGrey( const char *fname, int k=1 ); // сохранить в сером виде с умножением всех элементов на k
При этом числа меньшие 0 заменяются на 0, большие 255 – на 255.
Если задан параметр k, то перед сохранением все элементы матрицы будут умножены на него.
Есть возможность прочитать несжатый серый tiff-файл, глубина цвета может быть как 8 бит, так и 16:
int loadTifSimple(const char *fname);
// читаем серый tiff-файл без сжатия по-простому, returns error code
Иногда нам не надо загружать весь bmp-файл, а требуется лишь некоторая его часть. Это могут выполнить следующие методы:
void loadPart ( const char*fname, int x0, int y0, int dx, int dy);
void loadPartGrey(const char*fname, int x0, int y0, int dx, int dy);
При работе с компьютерной графикой нам часто нужны значения функции не только в целых точках, но и между ними. Эта возможность обеспечивается механизмом интерполяции:
double getInterp1( double x, double y ); // Билинейная интерполяция
double getInterp3( double x, double y ); // Бикубическая интерполяция
Если аргументы (x,y) отрицаетельны или превышают верхнюю границу, то они возвращаются в допустимый интервал, так же, как и в функции safeGet. Таким образом, ни при каких значениях аргументов ошибка не возникает.
Кроме того, имеется возможность "универсальной" интерполяции, где тип ("тривиальная", "билинейная" или "бикубическая") задается числовым параметром:
double getInterp ( double x, double y, int k=1 ); // universal interpolation k=0|1|3
Это может оказаться полезным, когда мы хотим проверить влияние метода интерполяции на результат расчётов, для смены метода интерполяции достаточно будет изменить числовой параметр k.
Копирование значений одной строки/столбца матрицы в другую строку/столбец:
void copyLine ( int yDst, int ySrc ); // копировать строку
void copyColumn( int xDst, int xSrc ); // копировать столбец
Копирование прямоугольного блока из матрицы a в текущую (this):
void copyBlock( matr &a, int xSrc, int ySrc, int xDst, int yDst, int dx, int dy );// this:=a[часть]
Заполнение одним значением строки, столбца, прямоугольного блока, круга, внешности прямоугольника:
void fillLine ( int y0, int v ); // заполнить строку значением v
void fillColumn( int x0, int v ); // заполнить столбец значением v
void fillBlock( int v, int x0, int y0, int dx, int dy );
void fillCircle( int v,int xr, int yr, int r );
void fillOuter( int x0, int y0, int x1, int y1, int v);
// заполнить внешность прямоугольника (x0,y0)-(x1,y1) значением v
Во многих алгоритмах требуется что-то сделать для всех точках отрезка. Обычно "все точки" понимаются как точки, построенных с помощью алгоритма Брезенхэма. Для этого у нес имеется класс edgeIterator:
class edgeIterator{...} // проход по точкам отрезка
Вот пример его использования:
edgeIterator ei(20, 120, 120, 30); // отрезок (20,120)-(120,30) do m(ei.Y(), ei.X()) = 255; while (!ei.next());
Этот класс реализован в самом начале файла iMatrix.cpp.
С его использованием реализованы следующие функции.
Рисование отрезков, минимум/максимум/среднее на отрезке
void drawEdge(int x0, int y0, int x1, int y1, int c);
// прорисовать отрезок [(x0,y0),(x1,y1)] значением c
double midEdge(int x0, int y0, int x1, int y1);
// mid value on the edge (x0,y0)-(x1,y1)
double midEdg2(int x0, int y0, int x1, int y1);
// mid*sqrt(len)
int minEdge(int x0, int y0, int x1, int y1, int &x2, int &y2);
// min value on the edge (x0,y0)-(x1,y1)
int maxEdge(int x0, int y0, int x1, int y1, int &x2, int &y2);
// max value on the edge (x0,y0)-(x1,y1)
Нахождение максимума/минимума:
int minimal(); // minimal value
int maximal(); // maximal value
int minimal(int &x_, int &y_); // minimal value
int maximal(int &x_, int &y_); // maximal value
Две последние функции позволяют найти сам экстремум и точку в которой он достигается. Если таких точек несколько, возвращается первая из них.
Максимум/минимум в отдельной строке/столбце ищут следующие функции:
int minLin(int &x_, int y_); // minimal value in line y, (x,y) - point
int maxLin(int &x_, int y_); // maximal value in line y, (x,y) - point
int minCol(int x_, int &y_); // minimal value in column x, (x,y) - point
int maxCol(int x_, int &y_); // maximal value in column x, (x,y) - point
double mid(); // среднее арифметическое элементов матрицы
Среди 9-ти соседей точки (x0,y0) найти точку (x1,y1) с наименьшим/наибольшим значением.
Возвращаем найденное значение:
int minNeib(int x0, int y0, int &x1, int &y1);
int maxNeib(int x0, int y0, int &x1, int &y1);
r-окрестностью точки будем называть квадрат размера (2r+1)*(2r+1) с центром в нашей точке.
Будет ли точка строгим локальным максимумом/минимумом в r-окрестности:
bool localMax(int x, int y, int r = 1);
bool localMin(int x, int y, int r = 1);
Значение текущей матрицы в каждой точке устанавливаем равным наибольшему/наименьшему значению матрицы a в r-окрестности соответствующей точки:
void minNeib( matr &a, int r );
void maxNeib( matr &a, int r );
Проверка того, что на сторонах квадрата со стороной 2*r+1 с центром (x,y) все значения равны 0:
bool emptyBorder(int x, int y, int r); // на сторонах квадрата со стороной 2*r+1 пусто?
Если на сторонах квадрата со стороной 2*r+1 с центром (x,y) все значения равны 0, то и значение в точке обнуляем:
void clearSmall(int r); // обнулить маленькие области
Количество элементов:
int countVal( int val ); // количество элементов, равных v
int countValI( int val0, int val1 ); // количество элементов x: val0≤x≤val1
Замена:
int changeVal(int v1, int v2); // заменить v1 на v2. Возвращает количество замен
int changeVal2(int v1, int v2, int v3); // заменить значения из интервала [v1..v2] на v3. Возвращает количество замен
void clip( int min_, int max_ ); // значения, меньшие min заменяем на min, max - аналогично
void normalize( int k ); // привести значения в матрице к отрезку [0..k]
void Mod( int k ); // привести значения в матрице mod k (0..k-1)
Одна из основных операция в компьютерной графике - сглаживание данных.
В нашем модуле сглаживание может быть трех типов:
Треугольным сглаживанием радиуса r называтся сглаживание с ядром K(x,y) = k(x)*k(y), где
{ r=|x|/ r*r, если |x|<r
k(x) = {
{ 0 иначе.
Например, при r=4 таблица значений фунции k(x) такова:
x : -5 -4 -3 -2 -1 0 1 2 3 4 5 k(x) : 0 0 1/16 2/16 3/16 4/16 3/16 2/16 1/16 0 0
График этой функции является треугольником, поэтому сглаживание и называется треугольным.
Наиболее эффективным и в тоже время простых является треугольное сглаживание,
однако многие, не вникая в детали, предпочитают обычное гауссово.
Отметим, что треугольное сглаживание с радиусом 2r примерно соответствует
гауссову сглаживанию с радиусом r.
Реализуется сглаживание методом:
void smooth( int r, int kind=1 ); // smoothing with radius r
Алгоритм сглаживания неплохо оптимизирован, как по скорости работы, так
и по минимизации погрешностей округления.
Поэтому можете смело сглаживать с большим радиусом (50, 100, ...),
время работы останется приемлемым.
Не забывайте, что исходные данные в компьютеной графике - целые, поэтому при сглаживании могут появляться различные ненужные артефакты. Для того, чтобы этого избежать, умножьте исходную матрицу перед сглаживанием на некоторый коэффициент, 16 или 256:
matr a; // описали матрицу
a.loadBMPGrey("lena.bmp"); // прочитали картинку
a.mult(256); // умножили все числа на 256
a.smooth(23, 1); // сгладили с треугольным ядром с радиусом 23.
void mult( int k); // this *= k
void mult( matr &a); // this(x,y) *= a(x,y) поэлементно
void div ( int k); // this /= k
void add( matr &a); // this += a
void add( matr &a, int k); // this += a*k
void addV( int r); // this[*,*] += r
void sub( matr &a); // this -= a
void addMult( matr &a, int k);// this += a*k
Следующие две функции копирует элементы матрицы a в текущую матрицу условно, точнее говоря, копируются только ненулевые элементы:
void mask(matr &a); // если a(x,y)!=0, то this(x,y):=a(x,y)
void mask(matr &a, int x0, int y0); // если a(x,y)!=0, то this(x0+x,y0+y):=a(x,y)
void addB(matr &a); // this += a побайтово
int sumRow( int y); // сумма элементов y-ой строки
int sumColumn( int x); // сумма элементов x-го столбца
Частные производные в точке (на 2 умножается, чтобы не было лишних округлений):
int dx( int x, int y); // 2*da/dx in the point
int dy( int x, int y); // 2*da/dy in the point
int dxx(int x, int y); // d2a/dxdx in the point
int dxy(int x, int y); // d2a/dxdy in the point
int dyy(int x, int y); // d2a/dydy in the point
double l2Grad( int x, int y); // length of gradient in the point
int mGrad(int x, int y, int h = 1); // morphological gradient in a point
// (max-min amoung (2*h+1)*(2*h+1) neigbour points)
int variat(int x, int y, int h = 1); // сумма модулей отклонений от центрального значение в квадрате (2*h+1)*(2*h+1)
double midVar(); // средняя разность между соседями
Краевые эффекты здесь не забыты! На границах матрицы вычисления проводятся по отдельным формулам!
Напомним, что морфологическим градиентом матрицы в точке называется разность наибольшего и наименьшего значений в квадрате 3*3 вокруг точки.
Частные производные во всей матрице:
void diffX(matr &a); // this:= 2*da/dx
void diffY(matr &a); // this:= 2*da/dy
void diffXX(matr &a); // this:= d^2a/dxdx
void diffXY(matr &a); // this:= d^2a/dxdy
void diffYY(matr &a); // this:= d^2a/dydy
void l2Grad(matr &a); // this:= length of gradient in each point(a)
void mGrad(matr &a, int h = 1); // this:= morphological gradient in each point(a)
void variat(matr &a, int h = 1); // this:= сумма модулей отклонений от центрального значение в квадрате (2*h+1)*(2*h+1)
Пусть f(x,y) — функция яркости изображения. Её градиент равен
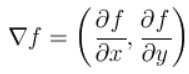
Квадрат длины градиента
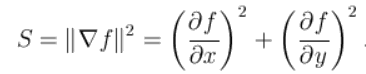
Точку назовем граничной, если производная S по направлению градиента функции f равна 0:

Градиент функции S равен
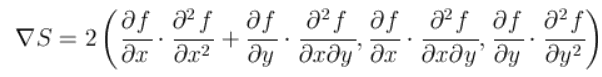
Таким образом, точку будем называть граничной, если R=(∇S,∇f)=0, где R=R(x,y) равно
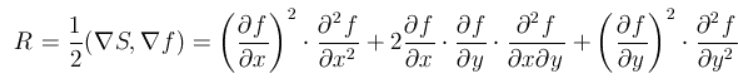
Более компактно запишем так:
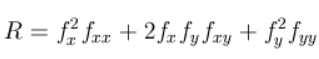
Если функция f(x,y) дважды непрерывно дифференцируема, то уравнение R(x,y)=0 задает на плоскости непрерывную кривую, овалы которой можно использовать в качестве основы для сегментации изображения.
Функция R(x,y) будет положительна в тех точках, где при сдвиге в направлении вектора градиента его длина увеличивается и отрицательна, если длина градиента при этом уменьшается. Можно сказать, что линия R(x,y)=0 отделяет темные точки (R>0) от светлых (R<0).
Рассмотрим методы вычисления функции R. Обозначим значения 9 соседних элементов матрицы через fij:
| f00 | f10 | f20 |
| f01 | f11 | f21 |
| f02 | f12 | f22 |
Приближённых значения для производных возьмём такие:
fxx = f21 - 2f11 + f01, fxx = (f00 - f20 - f02 + f22)/4, fyy = f12 - 2f11 + f10,
Тогда:
Определение.Пусть даны значения функции яркости в 9-ти соседних точках. Центральную точку будем называть яркой, если R-инвариант меньше 0 и темной в противном случае. Частные производные будем вычислять по указанным выше формулам, поэтому результат зависит только от девяти значений fij.
Замечание.Для корректного вычисления R-инварианта сглаженного изображения, его надо предварительно умножить на некоторую константу. При сглаживании с радиусом до 6 достаточно будет умножить на 16, при большем радиусе сглаживания лучше умножить на 256.
В нашем модуле R-инвариант матрицы в точке находится через методы:
double Rinvar (int x, int y); // R-инвариант в точке
int Rinvars(int x, int y); // (-1|0|1) Знак R-инварианта в точке
Для изменения размера изображения можно использовать следующие два метода:
void decrease( matr &a, int k ); // this := decrease size k times(a)
void resize( matr &a, int mx1, int my1); // this := resize(a) до (mx,my)
Если вы хотите округленить размер вниз до кратного k, можно использовать метод:
void roundSize( int k); // округлить размеры вниз до кратного k
Например, чтобы сделать оба измерения матрицы а чётными, надо выполнить:
a.roundSize(2);
Матрица не интерполируется, а просто у неё обрезается полоска справи и снизу.
Транспонирование
void transpose( matr &a); // this := transpose(a)
Существуют довольно эффективные (и сложные) алгоритмы транспонирования неквадратной матрицы
на месте, без выделения памяти. Здесь этого нет. По-простому.
Гистограммой матрицы будем называть массив, i-й элемент которого равен количеству появлений числа i среди элементов матрицы.
void historgrammK( int k0, int k1, int *hist ); // hist:= гистограмма значений k0..k1 матрицы
Перед выхзовом фукнции надо определиться с интересующим нас интервалом значений. Функция предполагает, что массив hist имеет размер не меньше 1+k1-k0.
Рассмотрим теперь использование квантилей.
void Quantile ( double p0, int &v0, double p1, int &v1 );
// (v0,v1):=квантили (p0,p1) распределения значений в матрице a
Допустим, что в матрице a
содержится функция яркости некоторого изображения. Часто приходится искать
самую яркую или самую темную точку изображения. Однако часто одной точки оказывается
недостаточно и требуется найти, например, 4% самых темных точек и 11% самых ярких.
Это можно выполнить следующим образом:
int v0, v1;
a.Quantile (0.04, v0, 0.11, v1 );
После выплнения этой команды в переменных v0, v1 будут записаны такие числа, что:
Пусть матрица a имеет тот же размер, что и текущая. Таким образом, мы имеем два набора чисел this->v[i] и a.v[i] одной и той же длины mx*my.
Метод MSE находит среднеквадратичное отклонение одного набора чисел от другого.
double MSE( matr &a ); // Mean Square Error (this,a)
Таким образом после выполнения
matr b;
b.copyFrom(a);
b.addV(7);
double mse = a.MSE(b);
Другая часто применяемая величина PSNR может быть получена как
double psnr = noise2psnr(mse);
Энтропия. Пусть в матрице a число 0 встречается p[0] раз, число 1 - p[1] раз и т.д., число 255 - p[255] раз. Тогда энтропией матрицы назовем сумму по всем i таким, что p[i]>0:
255 SUM p[i]*ln(p[i]); i=0
Для вычисления энтропии служит метод
double entropy (); // Энтропия: sum p[i]*log(p[i])
Смысл энтропии состоит в том, что это наименьшее количество битов, требуемое для кодирования матрицы в предположении, что её элементы не зависят друг от друга.
Коэффициенты Фурье. Коэффициенты Фурье, особенно двумерные,
применяются во многих разделах компьютерной графики.
Наш класс может вычислять двумерные коэффициенты Фурье как для всей матрицы,
так и для её прямоугольного участка:
double Fourier(int i, int j);
// ij-Fourier coefficient of a whole matrix
double Fourier(int i, int j, int x0, int y0, int dx, int dy);
// ij-Fourier coefficient of block of matrix
Для некоторых экспериментов желательно иметь матрицу, элементы которой линейно зависят от координат: a(x,y) = a0 + x*ax + y*ay. Построение такой матрицы обеспечивается методом
void setLinear( int mx, int my, int minV, int maxV, double ax, double ay, double a0);
Например, в результате выполнения
matr a;
a.setLinear(5, 8, 0, 255, 50, -40, 200);
a.saveText("a.txt");
5 8
200 250 255 255 255
160 210 255 255 255
120 170 220 255 255
80 130 180 230 255
40 90 140 190 240
0 50 100 150 200
0 10 60 110 160
0 0 20 70 120