Подготовил Е.В.Соколов
Условия задач : 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс| + + + | К | О О | Л Л Л | Я Я Я Я |
| 1 | 9 | 9 | 6 |

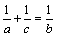
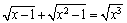
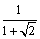 .
В каком случае достигается равенство?
.
В каком случае достигается равенство?
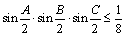 .
Когда достигается равенство?
.
Когда достигается равенство?
| 1 место | Белов Дмитрий | школа № 33 (5 кл.) |
| 2 место | Шаповалова Валентина | лицей <Гармония> (5 кл.) |
| 3 место | Мольков Дмитрий | школа № 33 |
| Рябинин Сергей | школа № 4 | |
| Поощрительная премия | Антонов Евгений | школа № 7 |
| Гулаев Андрей | школа № 36 | |
| Ковалев Артем | школа № 7 | |
| Рябиков Александр | школа № 7 |
| 1 место | Ульянов Федор | школа № 33 |
| 2 место | Моисеев Игорь | лицей <Гармония> |
| Шаповалова Валентина | лицей <Гармония>(5 кл.) | |
| 3 место | Воробушков Василий | школа № 30 |
| Гудков Алексей | школа № 33 | |
| Проворов Антон | школа № 64 | |
| Поощрительная премия | Ананьев Сергей | школа № 20 |
| Волков Сергей | школа № 6 | |
| Городенцев Василий | школа № 6 | |
| Гостев Алексей | школа № 6 | |
| Ершова Светлана | школа № 21 | |
| Карманова Ира | школа № 29 | |
| Копятин Денис | школа № 22 | |
| Кузьмина Елена | школа № 6 | |
| Лысов Женя | школа № 22 | |
| Лютер Александр | школа № 36 | |
| Мартюшов Андрей | школа № 39 | |
| Никитова Анна | школа № 39 | |
| Пискунова Елена | школа № 30 | |
| Сизова Татьяна | школа № 6 | |
| Стройнов Евгений | школа № 39 | |
| Шахнис Илья | школа № 29 | |
| Шуляев Алексей | школа № 22 | |
| Щукина Наталья | школа № 6 |
| 1 место | Васильев Дмитрий | школа № 21 |
| Жлудов Вячеслав | школа № 21 | |
| 2 место | Бакшин Алексей | школа № 30 |
| 3 место | Ефремов Андрей | школа № 21 |
| Филатов Алексей | школа № 30 | |
| Поощрительная премия | Пояскова Анастасия | школа № 22 |
| Гадалов Александр | школа № 6 | |
| Шнеерсон Вера | школа № 30 |
| 1 место | Хашина Екатерина | школа № 33 |
| 2 место | Филатов Евгений | школа № 33 |
| 3 место | Моругин Сергей | школа № 4 |
| Иванов Денис | школа № 22 | |
| Муницына Мария | школа № 33 | |
| Филиппова Светлана | школа № 33 | |
| Поощрительная премия | Битеряков Олег | школа № 30 |
| 2 место | Хрунов Алексей | школа № 22 |
| Тисков Александр | школа № 33 | |
| 3 место | Рожков Сергей | школа № 22 |
| Филатов Евгений | школа № 33 (9 кл.) | |
| Поощрительная премия | Антошин Дмитрий | школа № 33 |
| Губин Максим | школа № 22 | |
| Жуков Олег | школа № 33 | |
| Лазарук Сергей | школа № 67 | |
| Чистяков Павел | школа № 22 |
| 1 место | Часов Андрей | школа № 22 |
| Шаповалов Данил | школа № 33 (10 кл.) | |
| 2 место | Ефимов Виталий | школа № 33 |
| Зайцев Антон | школа № 33 | |
| Карпов Александр | школа № 22 | |
| Купцов Иван | школа № 33 | |
| Мокров Александр | школа № 33 | |
| Туровский Георгий | школа № 33 | |
| 3 место | Голубев Евгений | школа № 22 |
| Цыганков Илья | школа № 22 | |
| Поощрительная премия | Аксименко Евгений | школа № 22 |
| Бельский Антон | школа № 30 | |
| Завадский Алексей | школа № 42 | |
| Касаткин Роман | школа № 33 | |
| Котов Антон | школа № 22 | |
| Пирогов Дмитрий | школа № 33 | |
| Свислоцкая Юлия | школа № 33 |