Факультет математики и компьютерных наук, история

ИвГУ: Математический факультет.

49 городская математическая олимпиада

(7 декабря 1998 г.)

Подготовил Е.В.Соколов

Условия задач               :   6 класс        7 класс     8 класс     9 класс     10 класс     11 класс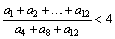  
Победители и призёры:   5-6 класс     7 класс     8 класс     9 класс     10 класс     11 класс  

6 класс


1. Двое ели сливы. Один сказал другому: <Дай мне свои 2 сливы, тогда у нас слив будет поровну>, на что другой ответил: <Нет, лучше ты дай мне свои 2 сливы, тогда у меня будет в 2 раза больше, чем у тебя>. Сколько слив у каждого?
2. Деньги, вложенные в акции известной фирмы, приносят ежегодно 20% дохода. За сколько лет вложенная сумма удвоится?
3. Существует ли дробь со знаменателем 20 большая, чем 4/13, и меньшая, чем 5/13 ?
4. Каждую сторону квадрата увеличили на 20%. На сколько % увеличилась его S? На сколько % увеличился его P?
5. У нескольких треугольников и четырехугольников 53 угла. Сколько треугольников и четырехугольников в отдельности, если всего их 15?
6. Выпишем подряд, начиная с 1, числа натурального ряда: 123456... 101112... . Какая цифра окажется на 1997 месте?

7 класс


1. На одном заводе работают слесарь, токарь и плотник по фамилиям: Борисов, Иванов и Семенов (профессии и фамилии названы в произвольном порядке). У слесаря нет ни братьев, ни сестер, и он самый младший из троих. Семенов женат на сестре Борисова, он старше токаря. Назовите фамилии слесаря, токаря и плотника.
2. Может ли натуральное число уменьшиться в 1998 раз, если зачеркнуть несколько его последних цифр? Если это возможно, то укажите все такие числа.
3. Найти наименьшее натуральное число, половина которого - полный квадрат, третья часть - полный куб, пятая часть - полная пятая степень.
4. На складе в большом количестве лежат ширлы, мырлы и дырлы. Ширла состоит из пяти шашек, мырла - из семи машек, дырла - из девяти дашек. Все шашки одинаковы, машки - тоже, одинаковы и все дашки. У Васи есть чашечные весы без гирь, и он хочет за одно взвешивание узнать, что тяжелее: две шашки или машка с дашкой. К сожалению, все изделия, имеющиеся на складе - неразборные. Помогите Васе!
5. Расстояние между деревнями A и B по шоссе равно 3 км. В деревне A - 100 школьников, в деревне B - 50 школьников. На каком расстоянии от деревни A надо построить школу, чтобы общее расстояние, которое придется пройти всем 150 школьникам было наименьшим?

8 класс


1. Остап Бендер организовал раздачу слонов населению. Явилось 20 человек, же-лающих получить слонов. Остап построил их по кругу, дал одному первого слона, его соседу слева - второго слона, затем одного человека пропустил, следующему дал слона, затем двоих пропустил, следующему дал слона, затем троих пропустил, и т.д., пока не раздал всех 1997 слонов. Скольким желающим не досталось ни одного слона.

2. Больной шахматный король стоит в центре клетчатой доски с размерами 5x5 клеток. Сможет ли он побывать на каждом поле, кроме исходного, ровно по одному разу и последним ходом вернуться на исходное поле, если делать два хода подряд в одном направлении он не в состоянии (т.к.больной )?
3. Три соседних озера время от времени меняют свой уровень. Каждые два из них связаны ручьями. Может ли случиться так, что в течение одного года вода текла из первого озера во второе больше 2/3 времени, из второго в третье - тоже больше 2/3 времени, а из третьего в первое - тоже 2/3 (Вода из одного озера течет в другое только в том случае, если уровень воды в первом озере выше уровня воды во втором)?
4. На продолжении наибольшей стороны AC треугольника ABC отложили отрезок CM такой, что CM = BC. Доказать, что ÐABM либо тупой, либо прямой.
5. Про числа a1, a2, ..., a12 известно, что 0 < a1 < a2 < ... < a12. Доказать, что

9 класс


1. Через n! обозначают произведение 1*2*3*...*n. Известно, что число 35! равно

10333147966386144929*66651337523200000000.

Найти цифру, замененную звездочкой.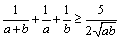
2. Доказать, что если при пересечении сторон четырехугольника с окружностью образуются 4 равные хорды, то суммы длин противоположных сторон этого четыреху-гольника равны между собой.
3. Можно ли выписать в строку 50 действительных чисел так, чтобы сумма любых 7 идущих подряд чисел была положительна, а сумма любых 11 идущих подряд чисел была отрицательна ?
4. Верно ли утверждение: сумма расстояний от любой точки, лежащей на стороне четырехугольника, до вершин этого четырехугольника не превосходит периметра этого четырехугольника ?
5. В одном городе есть несколько (более одного) автобусных маршрутов. При этом: Сколько автобусных маршрутов в этом городе. Приведите примерную схему.

10 класс


1. На доске выписаны все целые числа от 1 до двузначного числа N. Петя посчитал количество выписанных цифр, и оказалось, что оно записывается теми же цифрами, что и N, но в обратном порядке. Найдите все возможные значения N.
2. Имеется кучка из 97 орехов. За одну операцию разрешается любую из имеющихся кучек разделить на две. При этом, если образовались две неравные кучки, то взимается штраф один рубль. Какова наименьшая возможная сумма штрафа, которую придется заплатить, чтобы получить 97 кучек, по одному ореху в каждой?
3. На складе лежат 27 деталей, промаркированных первым или вторым сортом. Детали одинакового сорта весят одинаково, и каждая деталь второго сорта немного легче детали первого сорта. Известно, что ровно одна из деталей промаркирована неправильно. Покажите, что ее можно наверняка выявить за три взвешивания на чашечных весах без гирь.
4. Докажите, что для любых положительных a и b выполняется неравенство
5. На плоскости проведено пять прямых, из которых любые две пересекаются и никакие три не проходят через одну точку. Когда плоскость разрезали по этим прямым, среди полученных частей оказалось ровно пять углов (угол - это бесконечная часть плоскости, ограниченная двумя лучами с общей вершиной). Найдите сумму величин этих углов.

11 класс


1. По итогам математической олимпиады восемь победителей получили 97 книг. За более высокое место давали больше книг. Известно, что все победители получили разное число книг, причем за восьмое место книг было вручено не менее половины числа книг за первое место. Сколько книг получил каждый из восьми победителей? Найдите все решения и покажите, что других нет.
2. Дан жесткий квадратный проволочный контур со стороной 1 дм. Требуется разрезать его в четырех точках и спаять из полученных частей новый плоский замкнутый контур так, чтобы охватываемая им площадь увеличилась не менее чем на 5%. Как это сделать?
3. При каких натуральных n уравнение 2sin(nx) = tg(x) + ctg(x) имеет корень?
4. На каждой из десяти карточек написано по числу. Для каждого из 1023 непустых наборов этих карточек нашли сумму всех чисел, написанных на карточках этого набора. Известно, что не все эти суммы оказались целыми. Докажите, что целых сумм не более 511.
5. Могут ли два равных куба с общим центром быть расположены так, что каждая грань первого куба имеет общую точку с каждой гранью второго куба? (Считается, что точки на границе тоже принадлежат грани.)

Победители и призеры

6 класс

1 место Брулетова Алена лицей <Гармония>
Шаповалова Валентина лицей <Гармония>
2 место Куваев Александр лицей <Гармония>
Садовников Артем школа № 21
3 место Никологорская Анна лицей <Гармония>
Шабалин Алексей школа № 22
Поощрительная премия Бажан Сергей школа № 64
Морозов Денис школа № 21
Пономарев Илья школа № 33
Пулов Алексей школа № 15 (5 кл.)
Сазонов Андрей школа № 6
Санников Денис школа № 67 (5 кл.)
Хлебунов Михаил школа № 67 (5 кл.)
Цунаева Екатерина школа № 15 (5 кл.)
Черенков Максим школа № 6
Ширяева Екатерина школа № 15 (5 кл.)

7 класс

1 место Белов Дмитрий школа № 33 (6 кл.)
2 место Гулаев Андрей школа № 36
3 место Меженский Владимир школа № 22
Мольков Дмитрий школа № 33
Рябинин Сергей школа № 30
Сычев Антон школа № 33
Тремичев Иван школа № 6
Шаповалова Валентина лицей <Гармония> (6 кл.)
Поощрительная премия Бухон Сергей школа № 6
Морозов Иван школа № 6
Потемин Алексей школа № 6
Рубахин Александр школа № 6
Цыбин Роман школа № 6
Широков Василий школа № 6

8 класс

1 место Ульянов Федор школа № 33
2 место Абрамычев Михаил школа № 21
Куприянова Надежда школа № 33
Моисеев Игорь лицей <Гармония>
3 место Воробушков Василий школа № 33
Никитова Анна школа № 33
Пирожков Алексей школа № 33

9 класс

2 место Бакшин Алексей школа № 30
Гадалов Александр школа № 6
Лузина Мария школа № 22
Моисеева Ольга школа № 32
3 место Кононова Марина лицей <Гармония>
Соколов Алексей школа № 21

10 класс

1 место Филатов Евгений школа № 22
2 место Соколов Сергей школа № 33
Хашина Екатерина школа № 33
3 место Голубев Иван школа № 33
Косарев Илья школа № 33
Соловьев Алексей школа № 33
Филиппова Светлана школа № 33
Поощрительная премия Иванов Денис школа № 22
Крылов Иван школа № 22
Морулин Сергей школа № 22
Мочалин Михаил школа № 22
Муницина Мария школа № 33

11 класс

1 место Шаповалов Данил школа № 33
2 место Рожков Сергей школа № 22
Тараканова Елена школа № 30
Тисков Александр школа № 33
Фомин Павел школа № 33
3 место Губин Максим школа № 22
Корхов Алексей школа № 1
Попадюк Александр школа № 36
Хрунов Алексей школа № 22
Всего в олимпиаде приняло участие 867 человек, в т.ч.:

ИвГУ: Математический факультет. Главная страница