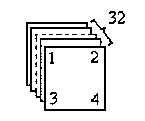


| { |
|
|
=-y2+2y+1 |
| { |
|
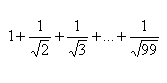
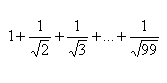
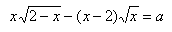
| 1 место | Куцевал Виталий | 6 класс | лицей №22 | |||||||||||||||||||||||||||||||||
| Кирьянов Антон | 5 класс | лицей №30 | ||||||||||||||||||||||||||||||||||
| 2 место. | Сироткин Алексей | 6 класс | лицей №35 | |||||||||||||||||||||||||||||||||
| Сычев Денис | 5 класс | лицей №33 | ||||||||||||||||||||||||||||||||||
| Козлова Наталья | 5 класс | лицей №33 | ||||||||||||||||||||||||||||||||||
| 3 место | Лобанов Андрей | 6 класс | лицей №33 | |||||||||||||||||||||||||||||||||
| Миронов Андрей | 5 класс | лицей №33 | ||||||||||||||||||||||||||||||||||
Поощрительные премии
| Шумилов Александр | 6 класс | школа №30
| Кувальцева Юлия | 6 класс | школа №4
| Виноградова Вера | 6 класс | школа №67
| Архипова Анна | 6 класс | школа №5
| Киреев Ярослав | 6 класс | школа №4
| Мудайар Руслан | 6 класс | школа №4
| Липина Мария | 6 класс | школа №5
| Баранов Андрей | 6 класс | лицей №33
| Челнокова Лидия | 6 класс | школа №4
| Бурдин Артём | 6 класс | лицей №33
| Гамов Георгий | 6 класс | школа №1
| Нефедов Данила | 6 класс | школа №33
| |
| 1 место | Калибин Борис | Гармония |
| 3 место | Горнушкина Ольга | школа №35 |
| 3 место. | Лопатин Илья | школа №21 |
| Сорокин Игорь | школа №22 | |
| Слободян Александр | школа №22 | |
| Поощрительные премии. | ||
| Куликова Евгения | лицей № 22 | |
| Краснов Александр | школа № 63 | |
| Баранов Олег | школа № 18 | |
| Казаков Иван | школа № 36 | |
| Костин Артём | школа № 26 | |
| Крайнев Алексей | школа № 21 |
| 1 место. | Харин Максим | лицей № 22 |
| 2 место. | Разумовский Роман | "Гармония" |
| 3 место. | Смирнов Алексей | лицей № 22 |
| Поощрительные премии. | ||
| Егорова Юлия | лицей № 22 | |
| Шуров денис | школа № 4 | |
| Каменев Михаил | школа № 29 | |
| Фомина Людмила | лицей № 33 | |
| Бычков Андрей | школа № 44 |
| 1 место. | Томин Дмитрий | лицей № 33 |
| 2 место. | Жамлиханов Тимур | лицей № 22 |
| Брулетова Алена | "Гармония" | |
| 3 место. | Бабенкова Юлия | лицей № 33 |
| Рубцов Андрей | лицей № 33 | |
| Белов Дмитрий | лицей № 33 | |
| Пономарёв Илья | лицей № 33 | |
| Поощрительные премии. | Тонкушин Антон | лицей № 33 |
| Либер Наталья | лицей № 22 | |
| Кульгавый Александр | лицей № 33 | |
| Капранов Владимир | лицей № 33 | |
| Мокеичева Мария | лицей № 33 | |
| Ефремов Алексей | лицей № 22 | |
| Костерин Антон | лицей № 33 | |
| Словесная Ю. | лицей № 33 | |
| Коношко Люба | лицей № 33 | |
| Сазанова | лицей № 33 | |
| Лебедева | лицей № 33 | |
| Дугина | школа № 49 | |
| Мазурина | школа № 22 | |
| Зуйков | школа № 30 | |
| Боброва | школа № 22 |
| 1 место. | Мольков Дмитрий | лицей № 33 |
| Рябинин Сергей | школа № 30 | |
| 2 место. | Тремичев Иван | школа № 6 |
| 3 место. | Гребнев Сергей | лицей № 22 |
| Харьков Олег | лицей № 22 | |
| Цыбиков Александр | лицей № 33 | |
| Поощрительные премии. | Казаков Александр | лицей № 33 |
| Корольков Валерий | школа № 44 | |
| Целищев Михаил | лицей № 22 | |
| Струнникова Ирина | лицей ИГХТУ | |
| Скоробогаткин Дмитрий | школа № 6 | |
| Рубахин Александр | школа № 6 | |
| Сычев Антон | школа № 33 | |
| Бардин Николай | школа № 7 | |
| Жидков Андрей | школа № 6 |
| 1 место. | Воробушков Василий Владимирович | лицей № 33 |
| Моисеев Игорь Георгиевич | Гармония | |
| Ульянов Федор Михайлович | лицей № 33 | |
| 2 место. | Никитова Анна Константинова | лицей № 33 |
| Кисляков Иван Юрьевич | лицей № 22 | |
| Пирожков Алексей Александрович | лицей № 33 | |
| Проворов Антон Александрович | лицей № 22 | |
| 3 место. | Гребнов Илья Викторович | лицей № 22 |
| Самылин Андрей Владимирович | лицей № 33 | |
| Куприянова Надежда Валерьевна | лицей № 33 | |
| Панина Ирина Анатольевна | лицей № 33 | |
| Сидун Евгения Леонидовна | лицей № 33 | |
| Поощрительные премии. | Голубев Иван Евгеньевич | лицей № 22 |
| Гудков Алексей Николаевич | лицей № 33 | |
| Дьякова Ольга Владимировна | лицей № 33 | |
| Шелест Дмитрий Сергеевич | лицей № 33 |
| Школа | 5 класс | 6 класс | 7 класс | 8 класс | 9 класс | 10 класс | 11 класс | Итого |
|---|---|---|---|---|---|---|---|---|
| гармония | 0 | 3 | 1 | 1 | 1 | 2 | 1 | 9 |
| лицей ИГХТУ | 0 | 0 | 0 | 0 | 0 | 2 | 5 | 7 |
| 1 | 3 | 3 | 0 | 3 | 3 | 0 | 2 | 14 |
| 2 | 0 | 3 | 0 | 0 | 4 | 1 | 1 | 9 |
| 3 | 0 | 2 | 2 | 3 | 4 | 2 | 2 | 15 |
| 4 | 0 | 11 | 4 | 3 | 5 | 3 | 0 | 26 |
| 5 | 0 | 7 | 8 | 6 | 3 | 1 | 3 | 28 |
| 6 | 0 | 1 | 0 | 3 | 5 | 4 | 2 | 15 |
| 7 | 0 | 0 | 0 | 2 | 0 | 4 | 0 | 6 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 |
| 14 | 0 | 4 | 2 | 1 | 3 | 4 | 1 | 15 |
| 15 | 0 | 4 | 2 | 4 | 1 | 0 | 3 | 14 |
| 18 | 4 | 5 | 4 | 4 | 1 | 1 | 1 | 20 |
| 19 | 0 | 2 | 4 | 0 | 4 | 4 | 3 | 17 |
| 21 | 0 | 3 | 2 | 6 | 5 | 2 | 6 | 24 |
| лицей22 | 5 | 6 | 3 | 10 | 12 | 4 | 8 | 48 |
| 23 | 0 | 0 | 4 | 4 | 7 | 0 | 2 | 17 |
| 26 | 0 | 8 | 3 | 4 | 2 | 2 | 0 | 19 |
| 27 | 0 | 0 | 1 | 2 | 1 | 0 | 0 | 4 |
| 28 | 0 | 0 | 1 | 0 | 0 | 4 | 0 | 5 |
| 29 | 0 | 0 | 3 | 1 | 0 | 0 | 0 | 4 |
| 30 | 2 | 5 | 5 | 2 | 1 | 1 | 2 | 18 |
| 31 | 0 | 0 | 0 | 0 | 0 | 5 | 5 | 5 |
| 32 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| лицей33 | 13 | 11 | 9 | 16 | 17 | 6 | 17 | 89 |
| 34 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 3 |
| 35 | 0 | 3 | 2 | 2 | 2 | 5 | 2 | 16 |
| 36 | 0 | 3 | 1 | 6 | 4 | 5 | 0 | 19 |
| 37 | 0 | 5 | 0 | 0 | 2 | 0 | 0 | 7 |
| 39 | 0 | 3 | 4 | 3 | 0 | 0 | 0 | 10 |
| 40 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 |
| 41 | 0 | 3 | 0 | 3 | 0 | 2 | 0 | 8 |
| 42 | 0 | 3 | 2 | 2 | 1 | 2 | 7 | 17 |
| 43 | 0 | 2 | 1 | 3 | 0 | 4 | 0 | 10 |
| 44 | 0 | 3 | 5 | 3 | 2 | 3 | 3 | 19 |
| 49 | 0 | 0 | 2 | 2 | 1 | 1 | 1 | 7 |
| 50 | 0 | 2 | 2 | 2 | 2 | 0 | 4 | 12 |
| 53 | 0 | 0 | 0 | 5 | 2 | 2 | 2 | 11 |
| 54 | 0 | 0 | 1 | 0 | 0 | 2 | 0 | 3 |
| 55 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 56 | 0 | 3 | 0 | 0 | 2 | 0 | 1 | 6 |
| 61 | 0 | 3 | 2 | 1 | 2 | 2 | 2 | 12 |
| 62 | 0 | 3 | 0 | 4 | 4 | 2 | 2 | 15 |
| 63 | 0 | 0 | 1 | 2 | 3 | 2 | 1 | 9 |
| 64 | 0 | 2 | 4 | 1 | 1 | 0 | 2 | 10 |
| 65 | 0 | 0 | 0 | 3 | 1 | 0 | 4 | 8 |
| 66 | 0 | 4 | 2 | 3 | 3 | 3 | 2 | 17 |
| 67 | 0 | 6 | 4 | 6 | 11 | 2 | 8 | 37 |
| Итого | 29 | 129 | 93 | 126 | 122 | 85 | 109 | 693 |