4. Известно, что для некоторых простых чисел p и q
и натуральных чисел x и y таких, что
x <p, y <q, число
2. На большой доске написано число 1000!. Федя проделывает следующую операцию. Он выбирает число вида n!, являющийся делителем числа, записанного на доске, и прибавляет выбранное число к записанному на доске. Результат записывается на доске, а исходное число стирается. Докажите, что независимо от выбираемых чисел, на доске когда-нибудь появится число 2002!.
3. Пусть ABCD – тетраэдр, w – сфера, касающаяся всех его ребер. Две точки касания сферы w с ребрами тетраэдра ABCD соединим отрезком тогда и только тогда, когда они лежат на одной грани тетраэдра. Доказать, что сумма всех таких отрезков меньше, чем 3(Al + Bl + Cl + Dl), где l – центр сферы w.
4. Коэффициенты a, b и c квадратного уравнения
5. Дан треугольник ABC. Окружность w1 с центром на отрезке AB проходит через A и пересекает вторично отрезки AB и AC в точках A1 и A2 соответственно. Окружность w2 с центром на отрезке BC проходит через C и пересекает вторично отрезки BC и AC в точках C1 и C2 соответственно. Известно, что окружности w1 и w2 касаются в точке К внешним образом. Докажите, что углы A1КC1 и A2КC2 равны.
2. Окружность w проходит через вершины В, С и центр окружности, вписанной в треугольник АВС. Второй раз окружность w пересекает прямую АВ в точке В1, а АС – в точке С1. Докажите, что длины отрезков ВВ1 и СС1 равны.
3. Известно, что для некоторых простых чисел p и q и натуральных чисел x и y таких, что x <p, y <q, число
| p | q | |
| | + | |
| x | y |
4. Пусть ABCD – выпуклый четырехугольник; SAB, SBC, SCD, SDA – окружности, построенные на сторонах AB, BC, CD и DA соответственно как на диаметрах. Известно, что SAB касается SCD, SBC касается SDA. Докажите, что ABCD – ромб.
5. Существуют ли четыре многочлена, такие, что сумма любых трех из них имеет хотя бы один корень, а сумма любых двух не имеет корней?
1. Известно, что хотя бы один из трехчленов x2 + ax + b , x2 + a2x + b2 , x2 + a3x + b3 , ... имеет вещественные корни. Докажите, что из этого множества трехчленов можно выбрать бесконечно много трехчленов, имеющих вещественные корни.
2. Число, написанное на доске, либо удваивается, либо из него вычитается единица. после нескольких таких операций из числа 1 было получено число 2002. Докажите, что в некоторый момент на доске было написано число с цифрой 3.
3. В треугольнике АВС угол С – прямой, СD – высота. Биссектрисы углов АВС и АСD пересекаются в точке М, а биссектрисы углов ВАС и ВСD – в точке N. Докажите, что длина отрезка МN равна радиусу вписанной в треугольник АВС окружности.
4. Известно, что для некоторых простых чисел p и q
и натуральных чисел x и y таких, что
x <p, y <q, число
| p | q | |
| | + | |
| x | y |
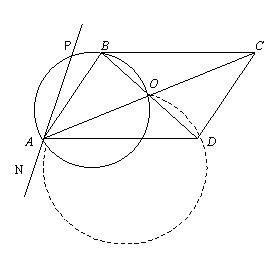
5. Пусть О – точка пересечения диагоналей параллелограмма АВСD, Р – вторая точка пересечения окружности, проходящей через точки А, О, В с прямой ВС (см. рис.). Докажите, что прямая АР касается окружности, проходящей через точки А, О, D.
1. По кругу стоит 2001 коробка. В каждой коробке лежат черные и белые шарики, а на коробке написано, сколько в ней черных шариков и сколько – белых. Игорь хочет переложить из каждой коробки по одному шарику в следующую коробку (по часовой стрелке) так, чтобы обе надписи на каждой из коробок стали неверными. Удастся ли ему это?
2. Докажите, что любой прямоугольник можно разрезать на 5 попарно различных равнобедренных треугольников.
3. Существует ли трехзначное число А, равное сумме двух чисел: суммы цифр числа А и произведения цифр числа А.
4.Восстановите с помощью циркуля и линейки треугольник АВС по трем точкам: D, Е, М, где D и Е – середины высот АН и СР треугольника АВС, М – середина стороны АС.
5.Дано выражение, содержащее 999 дробей:
| 1 | 2 | 3 | 999 | |||
| | * | | * | | * ... * | |
| 2 | 3 | 4 | 1000 |
В олимпиаде приняли участие 107 школьников 8 - 11 классов. Из них 61 человек из Ивановских школ и 46 из районов области. Олимпиада проходила один день (7 февраля) в течении 5 часов.
Первой премии жюри не присуждало
Пpедседатель жюpи олимпиады Н.Г.Косаpев