Число пи
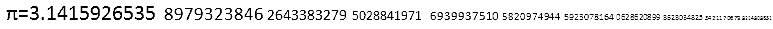
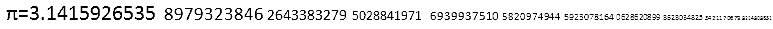
Неофициальный праздник любителей математики - «День числа пи» отмечается ежегодно 14 марта. Этот праздник придумал в 1987 году физик Лари Шоу из Сан-Франциско который подметил, что в американской системе записи дат (месяц/число) дата 14 марта — 3/14 — и время 1:59 совпадает с первыми разрядами числа π= 3,14159…. Обычно празднуют в 1:59 дня (в 12-часовой системе), но придерживающиеся 24-часовой системы считают, что в этот момент время 13:59, и предпочитают отмечать ночью.
По определению, число «пи» – это длина окружности, диаметр которой равен единице. Эквивалентно, число «пи» – это отношение длины окружности к ее диаметру. Следующая запись представляет собой десятичное разложение числа пи с 1000 знаками поле запятой:
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164
0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172
5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975
6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482
1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953
0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381
8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277
0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342
7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837
2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035
2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904
2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787
6611195909 2164201989
Впервые для обозначения этого числа греческой буквой π воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году. Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.
История числа π шла параллельно с развитием всей математики. То, что отношение длины окружности к диаметру одинаково для любой окружности, и то, что это отношение немногим более 3, было известно ещё древнеегипетским, вавилонским и древнегреческим геометрам. Самое раннее из известных приближений датируется 1900 годом до н. э.; это 25/8 (Вавилон) и 256/81 (Египет), оба значения отличаются от истинного не более, чем на 1 %.
Архимед,возможно, первым предложил математический способ вычисления π.
Для этого он вписывал в окружность и описывал
около неё правильные многоугольники. Принимая диаметр окружности за единицу,
Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины
окружности, а периметр описанного многоугольника как верхнюю оценку.
Рассматривая правильный 96-угольник, Архимед получил оценку
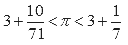
До II тысячелетия было известно не более 10 цифр π. Дальнейшие крупные достижения в изучении π связаны с развитием математического анализа, в особенности с открытием рядов, позволяющих вычислить π с любой точностью, суммируя подходящее количество членов ряда. В 1400-х годах Мадхава из Сангамаграма нашёл первый из таких рядов:
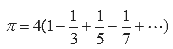
Этот результат известен как ряд Мадхавы—Лейбница, или ряд Грегори—Лейбница (после того как он был заново обнаружен Джеймсом Грегори и Готфридом Лейбницем в XVII веке). Однако этот ряд сходится к π очень медленно, что приводит к сложности вычисления многих цифр числа π на практике — необходимо сложить около 4000 членов ряда, чтобы улучшить оценку Архимеда.
Первую эффективную формулу нашёл в 1706 году Джон Мэчин
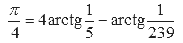
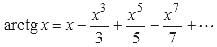
Теоретические достижения в XVIII веке привели к постижению природы числа π, чего нельзя было достичь лишь только с помощью одного численного вычисления. Иоганн Генрих Ламберт доказал иррациональность числа π в 1761 году, а Адриен Мари Лежандр в 1774 году доказал иррациональность π2. В 1735 году была установлена связь между простыми числами и π, когда Леонард Эйлер решил знаменитую Базельскую проблему (Basel problem) — проблему нахождения суммы числового ряда
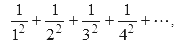
Эпоха цифровой техники в XX веке привела к увеличению скорости появления вычислительных рекордов. Джон фон Нейман и другие использовали в 1949 году ЭНИАК для вычисления 2037 цифр числа π, которое заняло 70 часов. Ещё одна тысяча цифр была получена в последующие десятилетия, а отметка в миллион была пройдена в 1973 году. Такой прогресс имел место не только благодаря более быстрому аппаратному обеспечению, но и благодаря алгоритмам. Одним из самых значительных результатов было открытие в 1960 году быстрого преобразования Фурье, что позволило быстро осуществлять арифметические операции над очень большими числами.
В начале XX века индийский математик Рамануджан обнаружил множество новых формул для π, некоторые из которых стали знаменитыми из-за своей элегантности и математической глубины. Одна из этих формул — это ряд:
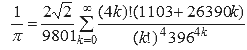
В то время как последовательность обычно повышает точность на фиксированную величину с каждым следующим членом, существуют итеративные алгоритмы, которые на каждом шагу умножают количество правильных цифр, требуя, правда, высоких вычислительных затрат на каждом из таких шагов. Прорыв в этом отношении был сделан в 1975 году, когда Ричард Брент (Richard Brent) и Юджин Саламин (Eugene Salamin) независимо друг от друга открыли алгоритм Брента — Саламина, который, используя лишь арифметику, на каждом шагу удваивает количество известных знаков. Алгоритм состоит из установки начальных значений
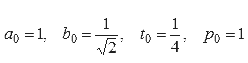
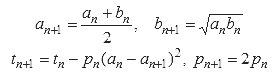
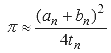
При использовании этой схемы 25 итераций достаточно для получения 45 миллионов десятичных знаков. Подобные методы позволили японскому математику Ясумаса Канада и его группе, начиная с 1980 года, установили большинство рекордов вычисления π вплоть до 206 158 430 000 знаков в 1999 году. В 2002 году Канада и его группа установили новый рекорд — 1 241 100 000 000 десятичных знаков. Эти вычисления состоялись 6 декабря 2002 года и длились более 600 часов. Хотя большинство предыдущих рекордов Канады были установлены при помощи алгоритма Брента — Саламина, вычисление 2002 года использовало две формулы типа мэчиновских, которые работали медленнее, но радикально снижали использование памяти. Вычисление было выполнено на суперкомпьютере Hitachi из 64 узлов с 1 терабайтом оперативной памяти, способном выполнять 2 триллиона операций в секунду.
В августе 2009 года учёные из японского университета Цукубо рассчитали последовательность из 2 576 980 377 524 десятичных разрядов
31 декабря 2009 года французский программист Фабрис Беллар на персональном компьютере рассчитал последовательность из 2 699 999 990 000 десятичных разрядов.
2 августа 2010 года американский студент Александр Йи и японский исследователь Сигэру Кондо рассчитали последовательность с точностью в 5 триллионов цифр после запятой.
Универсальность константы π показывает следующий пример Бюффона. На разлинованную равноудалёнными прямыми плоскость произвольно бросается игла, длина которой равна расстоянию между соседними прямыми, так что при каждом бросании игла либо не пересекает прямые, либо пересекает ровно одну. Можно доказать, что отношение числа пересечений иглы с какой-нибудь линией к общему числу бросков стремится к числу 2/π при увеличении числа бросков до бесконечности.
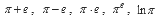
д.ф.-м.н., профессор, декан факультета математики и компьютерных наук Б.Я.Солон