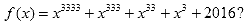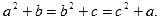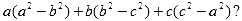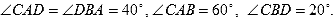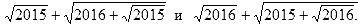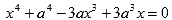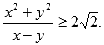на школьную страницу...
67 Мальцевская олимпиада по математике (2016 г.)
27 марта 2016 г. в ИвГУ (г.Иваново, ул. Ермака 37) прошла 67 Мальцевская олимпиада по математике
для школьников 8-11 классов г. Иваново и Ивановской области.
Мало баллов? Так ведь это МАТЕМАТИКА!
И ни одна решённая задача, и даже ни одна попытка решить её — не зря!
Есть ещё порох в пороховницах!
Задачи
8 класс
- На какое наименьшее число процентов нужно увеличить цену товара, чтобы,
продавая его потом с пятидесятипроцентной скидкой, не остаться в убытке?
- Медиана прямоугольного треугольника, проведённая к гипотенузе, разбивает
его на два треугольника с периметрами 18 и 25. Найдите стороны треугольника.
- Докажите, что
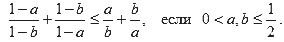
- Если
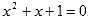 то чему равно значение многочлена
то чему равно значение многочлена
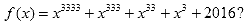
- Обращаясь к кассиру магазина, покупатель сказал: «Получите, пожалуйста, с меня
за две пачки соли по 9 рублей, за два куска мыла по 27 рублей, за три пачки сахара
и за 6 коробок спичек, но стоимость сахара и спичек я не помню».
Кассир выдал покупателю чек на 292 рубля. Взглянув на чек, покупатель вернул
его кассиру и сказал: «Вы несомненно ошиблись в подсчёте общей суммы».
Кассир проверил и согласился. Как покупатель обнаружил ошибку?
9 класс
- Числа a,b,c таковы, что выполняется равенство
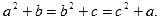
Какие значения может принимать выражение
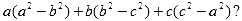
- В выпуклом четырёхугольнике ABCD
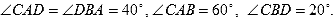
Найдите угол CDB.
- Петя заметил, что если число 2 приписать справа к любому натуральному числу,
то полученное число будет делиться на 2. То же самое происходит и с числом 5.
Найдите все такие натуральные числа n, меньшие 1000, после приписывания
которых справа к любому натуральному числу получается число, делящееся на n.
- Петя последовательно занумеровал числами от 1 до 1000 вершины 1000-угольника и,
начиная с первой, по кругу начал отмечать каждую пятнадцатую вершину
(1,16,31 и т.д.). Сделав, возможно, несколько кругов, он заметил,
что все отмечаемые вершины уже найдены, т.е. он отмечает только уже отмеченные ранее вершины.
Сколько вершин остались неотмеченными?
- Сравните без помощи калькулятора числа:
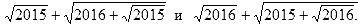
- Найдите все такие функции f(x), что
f(2x+1) = 4 x2 + 14x + 7.
10 класс
- Докажите, что произведение любых четырёх последовательных натуральных чисел,
увеличенное на единицу, является квадратом целого числа.
- Два города А и В расположены на берегу реки на расстоянии 10 км друг от друга.
Пароход проплывает из А в В и обратно за 1 час. Больше или меньше ему понадобится времени,
чтобы проплыть 20 км по озеру?
- На стороне ВС равнобедренного треугольника АВС (АВ=ВС) взяли точки М и N (N ближе к В, чем М)
такие, что NM=АМ и угол МАС равен углу ВАN. Найти угол САN.
- Докажите, что если a не делится на 2 и 3, то a2 делится на 24.
- Можно ли в таблицу 5×5 записать числа 1,2…, 25 так,
чтобы в каждой строке сумма некоторых из записанных в ней чисел была равна сумме остальных чисел этой строки?
11 класс
- Решите уравнение
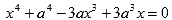
- Пусть xy =1 и x > y . Докажите неравенство:
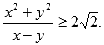
- В равнобедренном треугольнике АВС из середины Н основания ВС опущен
перпендикуляр НЕ на боковую сторону АС. Точка О делит пополам отрезок НЕ.
Докажите, что прямые АО и ВЕ перпендикулярны.
- Докажите, что при любом натуральном n число 9n - 8n - 1 кратно 64.
- В окружности с центром О дана хорда АВ и точка С на этой хорде такая,
что угол между прямыми АВ и ОС равен 45°. Докажите, что величина
AC2 + BC2 не зависит от выбора хорды АВ.
Разбор задач и награждение победителей — ровно через неделю, то есть
3 апреля в 10:00.
(фото кликабельны)
Результаты
А это – самые главные.
Конечно, не все. Те, кого удалось застать.

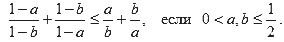
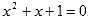 то чему равно значение многочлена
то чему равно значение многочлена