3.14.15 - Международный день числа π
Дорогие студенты факультета математики и компьютерных наук — будущие профессиональные математики, дорогие математики-любители и любители математики, дорогие прочие дети и взрослые! Каждый год 14 марта все, кто любит математику или математиков, отмечают один из самых необычных праздников — Международный день числа «Пи» (International π Day). Впервые День π был проведен в 1988 году в научно-популярном музее Эксплораториум в Сан-Франциско (San Francisco Exploratorium), а придумал этот неофициальный праздник годом ранее физик из Сан-Франциско Ларри Шоу, который подметил, что в американской системе записи дат (месяц / число) день 14 марта - 3/14 — совпадает с первыми разрядами числа π = 3,14... Если добавить время 1:59:26, то дата и время совпадают с первыми семью разрядами числа π = 3,1415926…. Обычно празднуют в 1:59:26 дня (в 12-часовой системе), но придерживающиеся 24-часовой системы считают, что в этот момент время 13:59, и предпочитают отмечать ночью.
Я предлагаю всем присоединиться к празднованию Дня π и прислать на факультетский e-mail: ivgu_matfak@mail.ru любые факты, связанные с числом π.
Мне показалась любопытной задача о квадратуре круга, которая тесно связана с числом π.
Квадратура круга — один из первых в истории математики случаев, когда человеческий разум долгое время буксовал перед нехитрой на первый взгляд задачей. Всего-то и требуется, что построить квадрат с площадью, равной площади данного круга, посредством циркуля и линейки. Около трёх тысяч лет (!) бесплодных усилий, испорченная репутация достойных учёных, сошедшие с ума армии фриков, драма, боль и ненависть, а в результате — лишь доказательство невозможности данного построения.
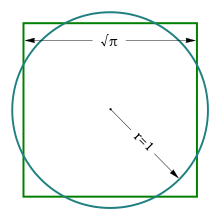
Если принять за единицу радиус круга и обозначить через x длину стороны искомого квадрата, то задача сводится к решению уравнения: x2=π, откуда: x=√π. Известно, что с помощью циркуля и линейки можно выполнять все 4 арифметических действия и извлекать квадратный корень (т.е. можно производить построения с помощью циркуля и линейки, используя отрезки, длины которых равны данным числам, и получить отрезок, длина которого равна результату соответствующей операции); отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины. Таким образом, неразрешимость этой задачи следует из неалгебраичности, а на самом деле – трансцендентность числа π, которая была доказана в 1882 году немецким математиком Карлом Линдеманом. Тем самым была закрыта известная с античных времен проблема квадратуры круга.
Итак, неразрешимость задачи о квадратуре круга связана с тем, что число π является трансцендентным и его нельзя построить с помощью циркуля и линейки. Однако на протяжении всей истории математики число π использовалось с той или иной точностью приближения.
Самое простое приближение для π полагает его равным 3 (несмотря на грубость этого приближения, его ошибка менее 5 %). Такое приближение использовалось, например, в Древнем Вавилоне в III–II вв. до н. э.: длину окружности находили по правилу, которое в современных обозначениях можно записать C = 3d, площадь круга находили по правилу S = C2/12. Значение π = 3 использовалось и древними иудеями: библейский автор упоминает, что при строительстве храма при царе Соломоне мастер Хирам из Тира в числе других храмовых украшений «сделал литое из меди море, – от края его до края его десять локтей, – совсем круглое,... и шнурок в тридцать локтей обнимал его кругом» (3 Цар 7, 23). Позже для более точных вычислений использовалось геометрическое приближение: от площади квадрата, описанного вокруг круга, отнимались площади треугольников с длиной стороны, равной трети стороны квадрата, получалось довольно точное значение π = 3 + 1/9 = 3,11.
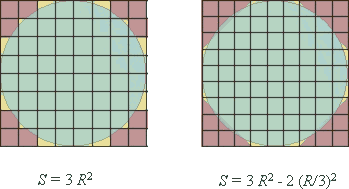
У древнегреческих математиков вопрос о численном значении π был не столь важным, по сравнению с проблемой квадратуры круга. Задача о квадратуре круга имела широкую известность не только среди математиков: например, о ней говорится в комедии Аристофана «Птицы».
Изучая задачу о квадратуре круга, Гиппократ Хиосский (V в. до н. э.) нашел некоторые случаи, когда с помощью циркуля и линейки можно найти квадратуру определенных частей круга, ограниченных кривыми линиями (а именно, двумя окружностями). Такие части называются луночками. Самый простой случай – это луночка между окружностью, описанной около равнобедренного прямоугольного треугольника, и другой окружностью, диаметром которой служит катет этого треугольника.
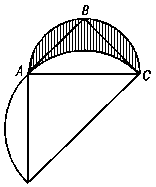
Древнейшие известные попытки собственно квадратуры круга принадлежат Антифонту и Бризону (V в. до н. э.). Антифонт последовательно вписывал в круг правильные многоугольники, каждый раз удваивая количество сторон. Бризон строил два квадрата – вписанный в окружность и описанный вокруг нее – и считал, что площадь квадрата, лежащего между ними, равна площади круга.

В дальнейшем именно вписанные и описанные правильные многоугольники стали активно применяться как для теоретических исследований, так и для конкретного вычисления числа π. Именно с помощью таких многоугольников было сформулировано строгое доказательство того, что площади кругов относятся как квадраты их диаметров, найденное, по-видимому, Евдоксом и приведенное в «Началах» Евклида. Архимед доказал, что площадь круга равна половине произведения длины окружности на ее радиус. Кроме того, с помощью вычисленных им периметров вписанных и описанных правильных многоугольников (от 6-угольника до 96-угольника) Архимед нашел, что:
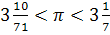
Таким образом, он не только нашел приближенные значения π, но и оценил точность этих приближений. Уже найденная Архимедом верхняя оценка, равная 22/7, дает приближение π с точностью 0,04 %. Эту дробь часто называют «архимедовым числом». Клавдий Птолемей, использовав правильный 720-угольник, нашел, что π ≈ 377/120, что составляет приблизительно 3,14167 (ошибка меньше 0,003 %).
Задача, похожая на квадратуру круга, фигурировала и в Древней Индии. В книге «Шулва-сутра», излагавшей правила строительства алтарей, построение круга, равновеликого данному квадрату ABCD, производится так. Вокруг квадрата описывается окружность; пусть перпендикуляр к отрезку AB, проходящий через центр окружности O, пересекает прямую AB и окружность в точках P и Q, а точка K делит отрезок PQ в отношении PK : KQ = 1 : 2. Тогда OK – радиус круга, равновеликого данному квадрату. Если a – сторона квадрата, то длина полученного радиуса
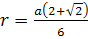
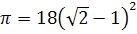
В более поздние времена в Индии использовались приближения для π, равные √10 (т. е. ≈ 3,162 – ошибка менее 1 %); 22/7 и даже 3,1416. Интересно наглядное доказательство предложения «площадь круга равна площади прямоугольника, стороны которого равны полуокружности и радиусу» у математика Ганеши (XVI в.). Как и в доказательстве теоремы Пифагора у Бхаскары, здесь все доказательство состоит из чертежа и слова «смотри». Ганеша делит круг на 12 секторов, а затем разворачивает каждый полукруг, состоящий из 6 секторов, в пилообразную фигуру, основание которой равно полуокружности, а высота – радиусу. Прямоугольник, о котором говорится в условии, получится при вставлении зубьев одной «пилы» в зазоры между зубьями другой.

Дальнейшее соревнование между математиками состояло в получении для числа π все большего
числа знаков после запятой. Рекорд для XIX в. поставил Уильям Шенкс,
нашедший в результате 707 знаков после запятой; в 1-ой половине XX в.
эти знаки часто воспроизводили в популярной литературе,
а архитекторы даже украшали ими свои сооружения (Дом занимательной науки в Ленинграде,
ныне Санкт-Петербург, 1934; Дворец открытий в Париже, 1937).
В 1945 г. результаты Шенкса были проверены на компьютере, и оказалось, что из его
знаков верны только первые 527. Компьютеры позволили существенно увеличить
количество точных цифр в десятичном разложении π, причем, если раньше вычислители
тратили на них многие годы, то теперь компьютеры справлялись с этим менее чем за день работы.
Этому также способствовало применение более эффективных алгоритмов на основании новых математических формул.
| Год | Вычислитель | Компьютер | Число верных знаков |
|---|---|---|---|
| 1949 | Дж. фон Нейман | ENIAC | 2 037 |
| 1958 | Ф. Женюи | IBM 704 | 10 000 |
| 1961 | Д. Шенкс, Дж. Ренч | IBM 7090 | 100 625 |
| 1973 | Ж. Гийу, М. Буйе | CDC-7600 | 1 000 000 |
| 1976 | Д. Х. Бейли | Cray-2 | 29 360 000 |
| 1987 | Я. Канада | NEC SX-2 | 134 217 000 |
| 1989 | Д. и Г. Чудновски | Cray-2, IBM 3090 | 1 011 196 691 |
| 1999 | Я. Канада, Д. Такахаси | HITACHI SR 8000 | 206 158 430 000 |
д.ф.-м.н., профессор, декан факультета
математики и компьютерных наук ,
Б.Я.Солон