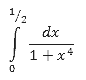Задачи для решения в системе "Максима"

На главную

Оглавление
Выражения
Графики
Анализ
Простые числа
Матрицы
Системы уравнений

1. Найдите сумму первых n членов гармонического ряда
       а) n=10,
       б) n=1000,
       в) n=100 000,
       г) Какое n надо взять, чтобы сумма получилась >20 ?.
   
2. Найдите сумму чисел 1/k² при k=1..n:
       а) n=10,
       б) n=1000,
       в) n=100 000,
       г) Бесконечность.
   
3. Какая цифра в десятичной записи числа π стоит на 47-м месте после запятой?
4. Сколько цифр в десятичной записи 100! ?
5. На сколько нулей оканчивается 100! ?
6. Вычислите значение (6+2*5^1/2)1/2-(6-2*5^1/2)^1/2.
7. Вычислите sin⁴(π/8) + cos⁴(3π/8) + sin⁴(5π/8) + cos⁴(7π/8).
8. Упростите выражение (1 + sin(2x) + cos(2x))/(1 + sin(2x) - cos(2x)).
9. Вычислить (1+sqrt(3))³⁷.
10. Вычислить (1+sqrt(-3))³⁷.
11. Разложите на множители многочлен x³-4x²+5x-2.
12. Разложите на множители многочлен (x+1)³⁶-1.

1. Построить график функции
       а) x/(x²-1)
       б) sin(1/x)
       в) x*cos(1/x)
       г) sin^3(x)
   
2. Постройте астроиду, задаваемую параметрическим уравнением x = cos(3t), y = sin(3t).
3. Постройте графики следующих функций в полярных координатах:
       а) спираль ρ(ϕ) = 1/ϕ,
       б) кардиоида ρ(ϕ) = 1 − cos ϕ,
       в) пятилепестковая роза ρ(ϕ) = sin(5ϕ).
   
4. Постройте график функции от двух переменных
        1/(x²+y²) + 2/((x-1)²+(y-1)²) – 3/((x+1)² + (y+2)²)

1. Вычислите предел последовательностей:
        а) lim ( n→∞) sqrt(n + 1) − sqrt(n),
        б) lim ( n→∞) sqrt(n² + n) − n,
   
2. Вычислите предел функции:
        а) lim (x→0+0) x^x,
        б) lim (x→0+0) (sin(x) - x+x³/6)/x⁵,
   
3. Вычислите производные для функций x^x, x^xx.
4. Вычислите неопределенные интегралы для следующих функций: x*ln(x), ln²(x), sin³(x), tg³(x).
5. Найдите 8 членов ряда Тейлора функции
        а) sin(x/(1+x²)).
        б) sin(sin(x)).
        в) tg(tg(x)).
        г) ln(ln(e+x)).
        д) (2-x³)/(2-x²+x³).
        е) sqrt(1+tg(x)).
   
6. Найдите линейные и квадратичные члены ряда Тейлора функции
        а) (x+y²)/(1+y+x²).
        б) sin(x+y²)/cos(y+x²).
        в) tg(x+y²)/(1+tg(y+x²)).
   
7. Вычислите определённый интеграл:
   
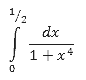
8. Найдите точки условного экстремума функций
        а) z=xy, если x+y=1.
        б) z=x/a + y/b, если x² + y²=1.
        в) z= x² + y², если x/a + y/b =1.
        г) u= xy + yz, если x² + y² =2, y+z=2, (x>0, y>0, z>0).
   

1. При каком наименьшем натуральном n число 1+2²ⁿ будет составным? Разложите его на множители.
2. Если числа n и n+2 простые, то они называются простыми числами-близнецами. Найдите все простые близнецы, не превосходящие 100. Подсчитайте количество пар простых близнецов, не превосходящих 10000.
3. Число называется совершенным, если сумма всех его делителей, кроме самого числа, равна этому числу, то есть divsum(n)=2n. Найдите первые 4 совершенных числа.
4. Два числа называются дружественными, если сумма всех делителей каждого из них (кроме самих этих чисел) равна другому числу, например, 220 и 284. Найдите все пары дружественных чисел, не превосходящих 10000.
5. Гипотеза Гольдбаха гласит, что любое четное число (кроме 2) можно представить в виде суммы двух простых чисел. Проверьте гипотезу Гольдбаха для всех чисел, не превосходящих 10⁵.
6. Простое число p называется безопасным, если (p-1)/2 – тоже простое. Найдите наименьшее безопасное простое число, превышающее 10¹⁰⁰.
7. Составное число n называется псевдопростым по основанию a, если a^n-1=1 mod n. Найдите первые 10 чисел,
        а) псевдопростых по основанию 2.
        б) псевдопростых по основанию 3.
        в) псевдопростых по основаниям 2 и 3 одновременно.
   
8. Найдите числа, меньшие 10000, псевдопростые по основаниям 2,3,5,7,11,13 одновременно.
9. Найдите все натуральные числа n (до 10⁹) такие, что
        а) 2^n-1=1 mod n².
        б) 3^n-1=1 mod n².
        в) 5^n-1=1 mod n².
        г) 7^n-1=1 mod n².
   
10. Разложить на множители a^k ± b^l + c, k=10,11,…
         а) a=7, «+», b=10, l=3, c=1,
         б) a=7, «-», b=10, l=3, c=1,
         в) a=11, «+», b=3, l=5, c=-1,
         г) a=11, «-», b=3, l=5, c=-1,
         д) a=2, «+», b=7, l=3, c=1,
         е) a=2, «+», b=7, l=3, c=1,
         ж) a=3, «-», b=7, l=3, c=-1,
         з) a=3, «-», b=7, l=3, c=1,
    
11. Пусть p=next_prime(7^k), q=next_prime(p+77777), n=pq. Разложить n на простые множители при k=10, 20, …
12. Пусть p[k] – простое число, следующее за k!. Найти p[k]-k при k=2,3,…
13. Пусть z = 1+sqrt(3) и пусть z^n = an + bn*sqrt(3); Найти НОД(an-1,bn) при n=101.
14. При n> 341 550 071 728 321 ≈ 3.4∙10¹⁵ функция проверки простоты числа primep(n) может ошибиться, а именно составное число признать простым. Найдите такое составное число в виде произведения двух простых чисел.
15. Найдите количество точек на эллиптической кривой по простому модулю:
         а) y²=x³ + 2x + 1 mod 17.
         б) y²=x³ + x + 2 mod 19.
         в) y²=x³ + x + 3 mod 23
         г) y²=x³ + x + 4 mod 23.
    
16. В какую степень надо возвести 2 mod p, чтобы получить 3?
         а) p=17.
         б) p=113.
         в) p=1103
         г) p=11003
    
17. Найдите количество простых среди 100 тысяч чисел, следующих за 10ⁿ
         а) n=6.
         б) n=10.
         в) n=100
         г) n=1000
    
18. Найдите количество чисел не имеющих делителей <1000, среди 100 тысяч чисел, следующих за 10ⁿ
         а) n=6.
         б) n=10.
         в) n=100
         г) n=1000
    

1. Пусть A – 3*3-матрица с элементами
        а) ((1,2,3),(4,5,6),(7,8,9)),
        б) (2,0,1),(4,0,1),((3,1,2)),
        в) (2,3,0),(3,1,1),((0,1,2)),
        г) (1,0,2),(2,1,1),((0,1,2)),
        д) (2,2,1),(3,1,1),((2,2,1)).
   Найдите:
        Определитель,
        обратную матрицу,
        характеристический многочлен,
        собственные вектора и собственные значения.
   
2. Пусть A – 3*2-матрица с элементами
        а) ((1,2,3),(4,5,6)),
        б) (2,0,1),((3,1,2)),
        в) (3,1,1),((0,1,2)),
        г) (1,0,2),((0,1,2)),
        д) (2,2,1),(3,1,1)).
   Для матриц B=A^t*A, C=A*A^t найдите:
        определитель,
        обратную матрицу,
        характеристический многочлен,
        собственные вектора и собственные значения.
   

1. Найдите численное решение уравнения cos x=x.
2. Решите уравнение x³ - x² - 11x + 15 = 0
3. Решите систему уравнений:
        xy=3
        x+y=5
   
4. Найдите многочлен 2-й степени, который в точках (-1,0,3) принимает значения (1, 2, -7) соответственно.
5. Найдите многочлен 4-й степени, который в точках (-3,-1,0,1,3) принимает значения (1, 2, -7, 0, 1) соответственно.
6. Найдите функцию вида (a0 +a1*x + a2*x²)/(b0+x), которая в точках (-3,-1,0,1) принимает значения (1, 2, -7, 0) соответственно.
7. Найдите плоскую кривую второго порядка, проходящую через точки
        (1,3), (2,-1), (3,0), ), (0,1), (-1,2).
8. Найдите плоскую кривую третьего порядка, проходящую через точки
        (1,3), (2,-1), (3,0), ), (0,1), (-1,2), (3,4), (-2,3), (2,3), (3,-1).
9. Пусть f = x³-6*x²+11*x-6.
        а) Решите уравнение f=0.
        б) Решите уравнение f=1.
        в) Решите уравнение f=0.001.
   
10. Найти корни, экстремумы, точки перегиба, асимптоты функции (x³-2*x²-5*x+6).
11. Найти корни, экстремумы, точки перегиба, асимптоты функции (x³-2*x²-5*x+6)/(x²-x-2).
12. Нарисуйте кривую второго порядка x^2 + 3*x*y + y^2 – 2*x – 3*y – 7 = 0. Определите её тип и приведите к каноническому виду.