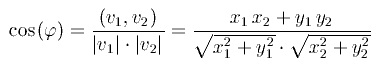
Угол между векторами плоскости на C++

Нахождение угла между векторами - самая обычная, часто возникающая задача в компьютерной графике. Пусть, например, нам даны два вектора на плоскости с целыми координатами v₁=(x₁ , y₁ ), v₂=(x₂ , y₂ ). Косинус угла между ними равен

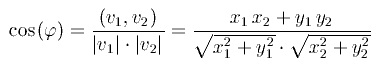
Запишем эту формулу в виде выражения на C++:

    (x1*x2+y1*y2)/(sqrt(x1*x1+y1*y1)*sqrt(x2*x2+y2*y2))

Осталось взять арккосинус. Оформим всё это в виде функции на C++:

double angle( int x1, int y1, int x2, int y2)
{ 
    return acos( (x1*x2+y1*y2)/(sqrt((double)x1*x1+y1*y1)*sqrt((double)x2*x2+y2*y2)));
}

Здесь (double)x1 приходится писать, чтобы явно указать компилятору, какой именно вариант функции sqrt использовать, а именно - квадратный корень из double.

Проверим:

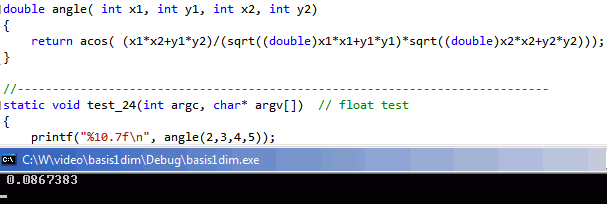
- всё вроде бы сходится. Проверка для самых различных значений x1,y1,x2,y2 дает ожидаемый ответ.

Но давайте найдем угол вектора с самим собой. Конечно, угол должен быть равен 0. Часто так и получается. Но проверим для вектора (2,3) :

Неужели компьютер сломался? Нет, конечно.

Так почему же? Всё просто.

    x1*x1+y1*y1=13, 
    sqrt(x1*x1+y1*y1)=3.6055512754640

    sqrt(x1*x1+y1*y1)*sqrt(x1*x1+y1*y1)=12.999999999999998

- чуть меньше 13.

Поэтому величина

    (x1*x2+y1*y2)/(sqrt(x1*x1+y1*y1)*sqrt(x2*x2+y2*y2)

будет чуть больше 1. Арккосинусу это, конечно же не понравилось. Вот он и выдал в результате -1.#IND, то есть ошибку.

Как же быть? Да ничего сложного, просто придется функцию несколько усложнить, например так:

double angle( int x1, int y1, int x2, int y2)
{ 
    double t = (x1*x2+y1*y2)/(sqrt((double)x1*x1+y1*y1)*sqrt((double)x2*x2+y2*y2));
    if     (t<-1) t=-1;
    else if(t> 1) t= 1;
    return acos(t);
}

Краткостью пришлось пожертвовать, зато - всегда работает!