В начало

С.И.Хашин

Сегментация изображений

Оглавление

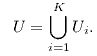
Изображение размера mx*my будем описывать тремя байтовыми матрицами R,G,B того же размера. Матрицы можно рассматривать как функции R(x,y), G(x,y), B(x,y) от целочисленных переменных 0 ≤x < mx,  0 ≤ y < my, принимающие целые значения от 0 до 255. Указанное множество целых точек на плоскости будем обозначать U_mx,my, или просто U.

В случае необходимости, с помощью некоторых интерполяционных формул, эти функции можно продолжить на всю плоскость и рассматривать их уже как отображения R² → R³. Чаще всего применяют билинейную или бикубическую интерполяцию, однако в каждом конкретном случае выбор интерполяционной формулы будем оговаривать отдельно.

Норма в цветовом пространстве

Таким образом, цвет пиксела является точкой в трехмерном цветовом (RGB) пространстве. Для определения расстояния между цветовыми точками введем в RGB-пространстве метрику с помощью евклидовой нормы. Простейший способ её определения — как суммы квадратов:

Однако, более правильным, по всей видимости, следует признать евклидову норму в YUV-пространстве,

то есть как квадратичную форму с матрицей

С другой стороны, вполне разумным, представляется определить норму как

Отметим, что выбор той или иной нормы в цветовом пространстве не окажет существенного влияния на изучаемые алгоритмы. Просто зафиксируем некоторый способ нахождения расстояния между точками в цветовом пространстве.

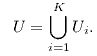
Кроме того вводим дополнительный, служебный сегмент U₀, состоящий из «несегментированных» точек. В начале алгоритма сегментации все точки относим к сегменту U₀, затем, в процессе сегментации каждая точка будет отнесена к одному из U_i, i ≥ 1.

При определении сегментации на подмножества U_i не было наложено никаких ограничений. На самом деле на них обычно накладываются определённые условия, например:

• Количество сегментов не превышает заданного предела.
• Границы сегментов должны быть сравнительно гладкими.
• Не должно быть слишком мелких сегментов.
• Сегменты должны быть связными.
• И т.д.

Определение. Сегментацию будем называть нормализованной, если:

• Номера сегментов идут подряд от 1 до K без пропусков.
• Размер сегмента не меньше размера предыдущего.

От любой сегментации можно ествественым способом перейти к нормализованной. Этот переход будем называть нормализацией.

Численная оценка качества сегментации

Что такое качество сегментации?

Понятие качества сегментации в общем виде формализовать трудно. Тем не менее, попробуем предложить некоторый вариант численной оценки. Это позволит сравнивать между собой различные программы и выявлять лучшие.

Рассмотрим пару полноцветных (TrueColor) изображений, не обязательно одинакового размера.

• Из второго изображения вырежем круг фиксированного радиуса (или, более обще, фиксированную кусочно-гладкую фигуру).
• Вклеим его в первое изображение опять же в случайное место.
• Сегментируем полученное изображение.
• Некоторые сегменты могут пересекаться как с внутренностью вклеенной фигуры, так и с её внешностью. Назовем такие сегменты ошибочными. Часть точек ошибочного сегмента принадлежит внешности фигуры, часть – внутренности. Меньшую часть из них назовем ошибочными точками.
• Качество сегментации будем обозначать двумя параметрами:
  • Средний размер сегмента (в точках).
  • 100% – (доля ошибочных точек по отношению к площади фигуры, %).

1. Предлагаемая далее программа позволяет готовить набор картинок требуемого вида (со вклеенными кругами) и тестировать заданную программу сегментации (exe- или bat-файл).
2. Алгоритмы сегментации должны быть оформлены в виде exe- (или bat-) файлов и работать в режиме «командной строки». Любой диалог с пользователем («Выберите файл для сегментации») категорически запрещен, т.к. программа будет вызываться автоматически. Файл для сегментации и желаемое количество сегментов передаются как аргументы в командной строке.
3. Желательно (хотя и не обязательно), программа должна уметь сегментировать изображение на различное заданное количество сегментов, например команда
   Segm_first.exe pict.bmp pict.txt 250
   сегментирует картинку pict.bmp примерно на 250 сегментов записывает результат в файл pict.txt. Сравниваются программы при примерно одинаковом количестве полученных сегментов.
4. Формат всех рассматриваемых файлов – BMP-24. Это простейший формат файла, его можно прочитать и сохранять без дополнительных библиотек, детальнее – см. в тексте.
5. Вклеивать круги лучше не совсем уж в случайное место. Его можно подобрать так, чтобы контраст с окрестностями был поменьше. Предлагаемая далее программа так и делает.

Segm_test2.pdf            – более подробное описание.
Segm_by_squares.exe – програма (Windows) для тривиальной сегментации (на квадраты).
segm_show.exe           – програма (Windows) для просмотра сегментации.

С вычислительной точки зрения сегментацией изображения размера mx*my будем называть матрицу того же размера из натуральных чисел. Каждое число обозначает номер сегмента (>0), к которому принадлежит точка. Такие матрицы сохраняются в текстовом файле вида

mx my комментарий
s00 s10 …
s01 s11 …
…

например, при сегментации файла размером 4*3:

4 3 ; в первой строке файла заданы размеры матрицы по x (4) и по y (3)
1 2 1 1
2 2 1 1
2 2 2 3

где цифры в теле матрицы означают номер сегмента (>0), к которому относится каждая точка.

Номера сегментов не обязаны идти подряд. Никакое упорядочение сегментов также не требуется.

Во многих алгоритмах требуется обойти все точки изображения в некотором (псевдо)случайном порядке. Пронумеруем точки изображения, точнее говоря, области U=U_mx,my целыми числами от 0 до mx*my-1. Таким образом, задача сводится к псевдослучайному обходу всех точек из множества {0, ..., N-1}, где N=mx*my.

Наиболее прост линейный метод. Выбираем натуральное число k, взаимно простое с N и начиная с произвольного x₀ находим следующее число по формуле:

Однако при обработке изображений такой метод дает не слишком хорошие результаты. Поэтому построим более сложный алгоритм, заменим в предыдущей формуле сложение на умножение. Воспользуемся следующим утверждением:

Предложение. Пусть p — простое число и a — первообразный корень по модулю p. Тогда среди чисел

Обходить в этом случае будем числа от 1 до N. Выберем простое число p большее N. Начиная с произвольного x₀ находим следующее число по формуле:

Если очередное число x_n+1 оказалось больше N, то его пропускаем и делаем следующую итерацию. Процесс повторяем до тех пор, пока вновь не получим x₀.

Пример. Пусть N=10. Выберем p=17, a=3. Пусть x₀=7. Тогда последовательность вычислений будет такова:

• 7 → 7*3 mod 17=4, x₁=4;
• 4 → 12 → 2, x₂=2;
• 2 → 6, x₃=6;
• 6 → 1, x₄=1;
• 1 → 3, x₅=3;
• 3 → 9, x₆=9;
• 9 → 10, x₇=10;
• 10 → 13 → 5, x₈=5;
• 5 → 15 → 11 → 16 → 14 → 8, x₉=8;
• 8 → 7, x₁₀=7=x₀, конец работы.

Таким образом, мы получили обход натуральных чисел от 1 до N=10 в псевдослучайном порядке:

Простое число p должно быть больше N, но не слишком значительно, так как количество «холостых» шагов равно p-N. Подходящие простые числа p и первообразные корни a можно приготовить заранее для всех возможных N, например, следующие:

Результаты работы многих сравнительно простых алгоритмов сегментации выглядят неудовлетворительно. Однако их можно существенно улучшить, причем методы улучшения можно применять практически ко всем алгоритмам.

Клеточный автомат

Идея клеточного автомата очень простая. Если точка принадлежит некоторому сегменту a, но большинство соседних принадлежат другому сегменту b ≠ a, то относим и эту точку к сегменту b.

У каждой внутренней точки (x,y) области U есть четыре соседних точки: вверх-вниз и вправо-влево. Помимо этого у точки можно рассмотреть и восемь соседних. Поэтому «большинство» можно искать как среди четырех, так и среди восьми соседей.

Более правильным следует признать «взвешенный» подход, когда четыре соседние точки (верх-низ-право-лево) рассматриваются с одним весом, а остальные четыре соседа с другим, меньшим весом. Учитывая, что расстояние до диагонального соседа в sqrt(2) раз больше, чем до ближайшего, то и вес его надо брать во столько же раз меньше. Чтобы не переходить к дробным числам, будет лучше взять вес четырех ближайших соседей равным 3, а четырех диагональных 2. Таким образом, сумма весов соседних восьми точек равна 20.

Поэтому правило клеточного автомата можно сформулировать так:

Если точка принадлежит некоторому сегменту a, но «взвешенное» большинство соседних принадлежат другому сегменту b ≠ a, то относим и эту точку к сегменту b.

Это правило надо применить одновременно ко всем точкам исходной матрицы. Фактически это означает, что надо строить новую матрицу того же размера с новой сегментацией и повторять этот процесс до тех пор, пока матрица не стабилизируется.

Практически того же самого результата можно добиться и с одной-единственной матрицей. Для этого на каждом шаге надо обойти все точки матрицы (в псевдослучайном порядке) и для каждой точки выполнить указанную выше операцию.

У точек на краю области U количество соседей меньше. Но для более однородного выполнения алгоритма можно распространить исходную сегментацию и на целые точки за пределом области U, например, считать, что точка (-1,y) относится к тому же сегменту, что и точка (0,y).

Сглаживание с помощью клеточного автомата — это сравнительно простой, но весьма надежный и эффективный инструмент. Его стоит использовать после почти любого метода сегментации.

Морфологическое сглаживание

Определение. Будем называть точку из сегмента U_i граничной, если одна из восьми соседних точек принадлежит другому сегменту. Множество всех граничных точек будем называть внутренней границей сегмента.

Определение. Внешней границей сегмента U_i будем называть множество точек не принадлежащих сегменту таких, у которых одна из восьми соседних принадлежит этому сегменту.

Определение. а) Замыканием сегмента будем называть присоединение к нему его внешней границы.
б) Эрозией сегмента будем называть перевод его внутренней границы в нулевой сегмент, то есть в несегментированные точки.

Будем предполагать, что сегментация нормализована, то есть размеры сегментов убывают с ростом номера.

Определение. Морфологическим сглаживанием сегментации будем называть последовательное замыкание всех сегментов начиная с 1-го и до последнего.

Связные сегменты

Определение. Сегмент называется связным, если из любой его точки можно добраться до любой другой по точкам сегмента, каждый раз переходя к одной из восьми соседних точек.

Вполне естественным требованием является связность каждого сегмента в сегментации.

Каждая область может быть разбита в непересекающееся объединение связных компонент. Поэтому от произвольной сегменатции можем перейти к сегментации со связными сегментами. Следует учитывать, что при этом количество сегментов может значительно (и непредсказуемо) вырасти. После перехода к связным сегментам придется проводить повторную нормализацию.

Удаление малых сегментов

Вряд ли целесообразно иметь сегменты размеров в 10-20 точек. От них лучше избавиться. Для этого сначала переведем точки таких сегментов в нулевой сегмент (то есть есть в несегментированные точки). Затем последовательно присоединяем точки нулевого сегмента к соседним. Для этого на каждом шаге рассматриваем точки внутренней границы нулевого сегмента и каждую из них присоединяем к тому сегменту, чья взвешенная сумма среди восьми соседей больше.

Предложенный алгоритм присоединения несегментированных точек к сегментам является простейшим, но не самым лучшим. Более правильным будет на каждом шаге выбрать пару 4-соседних точек (u,v) таких, что u лежит в нулевом сегменте, v — в ненулевом и цветовое расстояние между ними минимально среди всех таких пар. Теперь присоединяем точку u к сегменту точки v. Фактически, это есть алгоритм "сегментации через кристаллизацию", рассмотренный ниже.

Удаление перемычек

Иногда связный сегмент оказывается состоящим из нескольких массивных частей соединенных узкими перемычками. В таком сегменте каждую массивную часть стоит выделить в отдельный сегмент. Для этого с каждым сегментом выполняем следующие действия.

1. Несколько раз выполняем эрозию сегмента (т.е. переводим его внутреннюю границу в нулевой сегмент) до тех пор, пока сегмент остается связным, или пока не исчерпается заданное количество шагов.
2. Если сегмент остался связным, то восстанавливаем исходное состояние и заканчиваем работу.
3. Если же сегмент распался на несколько связных компонент, то преобразуем каждую из них в отдельный сегмент и начинаем к каждому из них присоединять соседние точки из нулевого сегмента, пока все они не исчерпаются.

Общая схема оптимизации

1. Сглаживание с помощью клеточного автомата.
2. Нормализация.
3. Морфологическое сглаживание.
4. Переход к связным сегментам.
5. Удаление сегментов размера меньше N₀.
6. Удаление перемычек.
7. Ещё раз нормализация.

Таким образом, единственным параметром оптимизации является минимальный размер сегмента N₀.

Топология сегментов

Для эффективной работы с сегментами требуется знать, какие сегменты являются соседними, какова величина общей границы, насколько близка два сегмента в разных смыслах. Для формализации этого введем понятия топологии сегментов. Пусть

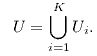
Определение. Обозначим через T_ij количество граничных пар для пары сегментов (U_i,U_j). Будем считать, что T_ii равно количеству всех граничных пар сегмента U_i, то есть

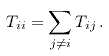
Определение. Обозначим через S_ij среднее цветовое расстояние между цветами граничных пар для пары сегментов (U_i,U_j). Будем считать, что S_ij=0, если нет общих пар или i=j.

Зная топологию сегментов можно эффективно сокращать из количество, то есть присоединять один сегмент к другому. А именно, для присоединения сегмента U_j к большему сегменту U_i (то есть i>j), потребуем, чтобы

Этот алгоритм будем называть топологической минимизацией количества сегментов.

Сегментация через триангуляцию

Рассмотрим следующий алгоритм сегментации изображения.

Шаг 1. Построение точек. В начале ставим 4 угловые точки. Затем добавляем по одной, ту - где длина градиента наибольшая, но не слишком близко к уже поставленным точкам, пока не получим нужное количество точек (а значит, и треугольников).

Шаг 2. Триангуляция Делоне построенной сети.

Оптимизация в этом случае, фактически не требуется. Однако, можно задать избыточное количество точек, получить избыточное количество сегментов и затем провести топологическую минимизацию сегментов до требуемого количества.

Segm_tri.exe – програма (Windows) для сегментации через триангуляцию.
Формат данных описан выше.

Пример. Рассмотрим изображение lena.bmp размера 512*512. В результате выполнение команды

Segm_tri.exe lena.bmp lena.txt 100

получим файл lena.txt с триангуляцией на 100 треугольноков и, дополнительно, segm1.bmp просто для иллюстрации результата:

Сегментация через кристаллизацию

Рассмотрим следующий алгоритм сегментации изображения. Пусть дано некоторое ожидаемое количество сегментов N.

Шаг 1. Выбираем удвоенное количество точек (2N), — центров будущих сегментов. Точки выбираем в тех местах, где усредненное значение длины градиента как можно меньше, причем точки не должны быть близко друг к другу.

Шаг 2. Наращиваем все сегменты из их центров. Каждый раз присоединяем к сегменту соседние точки, которые отличаются оп цвету наименьшим образом. В результате получаем сегментацию на удвоенное количество сегментов.

Шаг 3. Оптимизация.

Шаг 4. Топологическая минимизация количества сегментов до тех пор, пока не получим заданное их количество.

Segm_cry.exe – програма (Windows) для сегментации через кристаллизацию.

segm_brd.exe – програма (Windows) для сегментации по границам.

Замечание. Представленные прогаммы написаны исключительно в исследоваетельских целях, не оптимизированы ни по времени, ни по памяти. Для практического применения желательно брать более эффективные программы.

Непрерывная сегментация

Один из основных методов нахождения границ на изображении — «Canny edge detector».

Математическая суть его состоит в том, что точка называется граничной, если в ней достигается максимум модуля вектора градиента функции яркости в направлении роста функции, то есть в направлении самого вектора градиента. Переведем это определение на математическую основу.

Опишем алгоритм для одноцветного изображения, в реальности обычно берут функцию яркости:

Таком образом, пусть f(x,y) – функция яркости изображения, её градиент - это вектор с координатами

.

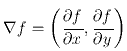Рассмотрим квадрат длины градиента

.

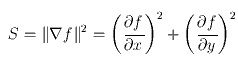Точку назовем граничной, если производная от S по направлению градиента функции f равна 0:

.

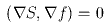Так как градиент функции S равен

.

.

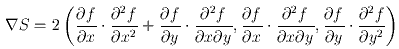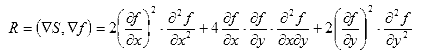Если функция f(x,y) дважды непрерывно дифференцируема, то уравнения R(x,y)=0 задает на плоскости непрерывную кривую, овалы которой можно использовать в качестве основы для сегментации изображения.

В случае табличного задания функции f(x,y), мы должны построить дважды непрерывно дифференцируемую интерполяционную функцию. Такую интерполяционную формулу построить нетрудно, однако результат оказывается не слишком удовлетворительным. Например, для изображения, состоящего из одной-единственной белой точки на черном фоне, границы, построенные таким образом имеют вид:

.

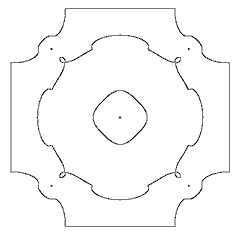Для реальных же изображений, количество получаемых овалов оказывается чересчур велико для практических применений.

Однако, вместо того, чтобы искать интерполяционный многочлен класса C², можно построить отдельные непрерывные интерполяционные формулы для производных функции f(x,y) первого и второго порядка. Для этого определим приближенные значения частных производных в целочисленных точках (x,y) по простейшим формулам

Предложенный способ построения граничных линий на изображении гораздо более естественен и устойчив. Например, в приведенном выше примере (белая точка на черном фоне) линия границы будет выглядеть так

.

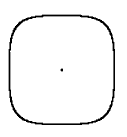Для примера рассмотрим небольшой кусок (размером 16*16) стандартного изображения «lena.bmp» («правый глаз»). Граница, найденная описанным выше способом в этом случае выглядит так:

Построенные таким методом «границы» разбивают плоскость на чересчур большое количество областей. Поэтому сгладим предварительно изображение с радиусом 2, получим следующие границы:

Таким образом, при практической реализации, предлагаемый подход следует дополнить еще двумя шагами:

• Сглаживание исходного изображения,
• Объединение построенных сегментов в более крупные.

Замечание. На каждом единичном квадрате функция R(x,y) является бикубической, то есть имеет степень 3 по x и по y. Коэффициенты этой функции в единичном квадрате зависят от значения функции f(x,y) в 16-ти соседних точках:

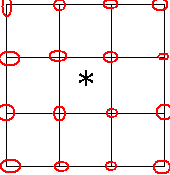
  f00 f01 f02 f03
  f10 f11 f12 f13
  f20 f21 f22 f23
  f30 f31 f32 f33

Непрерывная сегментация, явные формулы

  f00 f01 f02
  f10 f11 f12
  f20 f21 f22