Визуализация нейросети с двумя входами

Описание сети
Обучающая матрица
Описание программы
Пример результатов

Здесь мы рассматривам нейронные сети только одного специального вида.
Общий обзор нейронных сетей см, например, Википедия, MachineLearning.ru.

Нейроном будем называть функцию вида:

F = F(x,w) = F(w₀ + x₁w₁ ... + x_nw_n)

где x = (x₁, ..., x_n) — входы нейрона, w = (w₀, ..., w_n) — его внутренние параметры и F — активаторная, или передаточная функция.

Передаточные функции могут быть самые разные, мы рассмотрим лишь 4 из них:

F(x) = 0.5 + atan(x)/π;
F(x) = 1./(1+exp(-x));
F(x) = x<0 ? 0 : x;
F(x) = x<0 ? 0 : x<1? x : 1;

Нейронной сетью будем называть цепочку функций указанного выше вида.
Так как основным объектом нашей работы будут сети с 2-мя входами, выпишем формулы именно для этого случая.

     x₁ : входное значение (x-координата на плоскости),
     x₂ : входное значение (y-координата на плоскости),
     x₃ = F(w₃₀ + x₁w₃₁ + x₂w₃₂),
     x₄ = F(w₄₀ + x₁w₄₁ + x₂w₄₂ + x₃w₄₃),
     x₅ = F(w₅₀ + x₁w₅₁ + x₂w₅₂ + x₃w₅₃ + x₄w₅₄),
     ...,

Пусть сеть содержит N нейронов, их значения x₃, ..., x_N+2.

Общее количество внутренних параметров w_ij всех нейронов равно N(N+5)/2.

Значения последних K нейронов будем называть выходными значениями.

Нейронную сеть будем использовать для классификации входных векторов, а именно, если для данного входного вектора X=(x₀,y₀) среди K выходных значений (y₁,..., y_K) наибольшим будем y_k, то будем считать, что входная точка X относится к классу номер k.

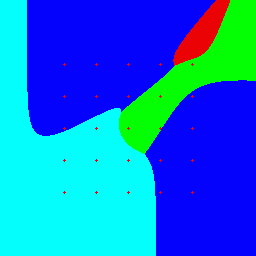
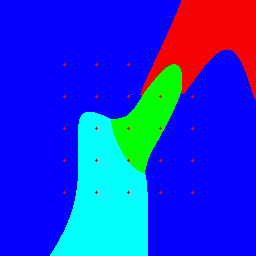
Результат классификации точек плоскости удобно изобразить в графическом виде, выделяя точки каждого кластера разным цветом. Например, ниже показаны результаты классификации точек квадрата (-0.5 ≤ x,y < 1.5) на 4 кластера для двух наборов внутренних параметров нейросети с 5-ю и 8-ю нейронами при передаточной фунции F(x) = 0.5 + atan(x)/π:

Если нам заранее известны номера кластеров k_i отдельных точек P_i на плоскости, мы можем попытаться подобрать внутренние параметры сети так, чтобы она выдавала правильный ответ на точках P_i.

Процесс подбора внутренних параметров будем называть обучением сети.

Один шаг обучения состоит из двух этапов.

Случайный выбор начальных значений параметров.
Минимизация, то есть изменение параметров, приводящее к минимизации целевой функции (функции потерь).

Способов минимизации много. Мы рассмотрим три из них.

Coord, Координатный спуск, по одной, по две, по три, по четыре координаты;
Grad, Градиентный спуск, метод обратного распространения ошибки;
Coord+Grad.

Обучающая матрица

Обучающие данные строятся на основе целочисленной матрицы A произвольного размера mx*my. Значения ≤0 в ней игнорируются. Координаты (x,y) нормализуются на отрезок [0,1]. Таким образом, элементу матрицы A_ij=k > 0 соответствует обучающая точка (x,y) = (j/mx, i/my) из единичного квадрата 0 ≤ x,y < 1, относящаяся к кластеру номер k.

При запуске программы обучающее множество будет представлено в графическом виде в bmp-файле teach.bmp размера 256*256.

Пример входной матрицы размера 2*2:

 2 2
 2 1
 1 2

Пример входной матрицы размера 3*3:

Пример входной матрицы размера 3*5:

Описание программы

Программа MaxNN_02.exe читает целочисленную входную обучающую матрицу A и строит полносвязную нейронную сеть с двумя входами и заданным количеством нейронов. Количество выходных значений равно максимальному значению в матрице.

Затем программа обучает построенную нейронную сеть таким образом, чтобы при всех (i,j) таких, что k=A[i,j]>0 сеть для точки (x,y)=(j/mx, i/my) выдавала значение k.

Текущее состояние сети полностью определяется действительным вектором w, содержащим внутренние параметры всех нейронов, длина вектора равна N(N+5)/2, где N &mbsp; количество нейронов.

Качество обучения описывается числами:

Nerr: Количество ошибок на обучающем множестве.
Ferr: Взвешенное количество ошибок. Вес ошибки на точке кластера обратно пропорционален его размеру.
S : Функция ошибок на обучающем множестве. Сумма квадратов отклонений вектора z от точного z', где z=SoftMax(y) и y — выходной вектор сети, то есть значения последних K нейронов.

Запуск

MaxNN_02.exe teachMatrix Nneur time fAct mmin maxW

where:

 teachMatrix - text file with teach (integer) matrix,
 Nneur       - the number of neurons 1,2,...
 time        - work time in seconds
 fAct        - type of activation function [1..4]
 mmin        - minimization type [1..3]
 maxW        - maximal possible of w[*]

Comments:
 1. Non-positive values in teach matrix are ignored.
 2. Let K is a maximal number in teachMatrix.
    Then the last K neurons are the output.
 3. Activation functions:
    fAct=1: 0.5 + arctan(x)/Pi
    fAct=2: 1/(1+exp(-x))
    fAct=3: x<0 ? 0 : x
    fAct=4: x<0 ? 0 : x<1? x : 1
 4. minimization type:
    mmin=1: Coordinate descent,
    mmin=2: Gradient descent (backpropagation),
    mmin=3: Coordinate + Gradient descent.
 5. The number Nneur  must be greater or equal than the
    largest value of the matrix of input matrix.

Один цикл работы программы состоит в случайном выборе внутренних параметров w_i из интервала [-8..8] и последующей их оптимизацией выбранным методом.

Программа выполняет такие циклы в течении заданного интервала времени и выбирает в качестве результата цикл с наименьшим количеством ошибок (Nerr), а при одинаковом количестве ошибок — с наименьшим значением функции ошибок (S).

Отслеживать текущие результаты удобно запустив файл view.html, который будет показывать их вместе с обучающим множеством в графическом виде. Окно обновляется автоматически каждые 5 секунд.

Пример запуска:

MaxNN_02.exe matrix5.txt 6  600 2 3 8

Исходные данные берутся из matix5.txt, строится полносвязная нейрнонная сеть из 6 нейронов с активаторной функцией 2 (1/(1+exp(-x))) и затем в течении 600 секунд выполняются попытки её обучить. В каждой попытке берётся случайный набор внутренних параметров и ищется минимум методом 3 (координатный + градиентный).

Матрица matrix5.txt:

После завершения работы программы (10 минут) в текущем каталоге остаются файлы:

prot.txt: файл с протоколом работы:

NeiroU::initXX, Ninp=2, Nneir=4, Nout=3, Nw=18
---------------------------
   1(3): Nerr= 6, Ferr=   1.000, S=   1.067: :   2.44947:   7.99755:  -7.99935:   7.94675:  -1.56349:  -7.99980:  -5.13109:  -1.94881:   0.37456:   7.99841:   5.78624:  -7.99911:  -7.99896:  -3.12359:   5.89210:   7.99990:  -7.99937:   2.17186:
   1(3): Nerr= 6, Ferr=   1.000, S=   1.067:
NeiroNetU, Ninput =2, Noutput=3, Nneirons=4, Nw=18, NteachPoins=25
Stype=3, fAct=2, Nerr=   6, Ferr=   1.00000, S= 1.0668350
       x[ 1] - input value (x-coord in plane)
       x[ 2] - input value (y-coord in plane)
       x[ 3] = f(  +2.449472   +7.997547*x[ 1]  -7.999346*x[ 2])
y[0] = x[ 4] = f(  +7.946747   -1.563491*x[ 1]  -7.999796*x[ 2]  -5.131092*x[ 3])
y[1] = x[ 5] = f(  -1.948814   +0.374564*x[ 1]  +7.998407*x[ 2]  +5.786244*x[ 3]  -7.999114*x[ 4])
y[2] = x[ 6] = f(  -7.998959   -3.123591*x[ 1]  +5.892096*x[ 2]  +7.999899*x[ 3]  -7.999368*x[ 4]  +2.171862*x[ 5])
--------------------------
   2(3): Nerr= 7, Ferr=   1.100, S=   1.080: :  -2.76741:   5.52041:  -7.99944:   4.39218:  -7.99999:  -4.92322:   6.59775:   2.02969:   7.99969:   3.51966:  -6.08820:  -7.99923:  -7.95475:   7.99845:  -4.13484:  -7.99990:  -7.99880:   7.99777:
   3(3): Nerr= 7, Ferr=   1.100, S=   1.080: :  -2.63783:   5.32466:  -7.99853:   4.26670:  -7.99975:  -4.72450:   6.89286:   1.89674:   7.99881:   3.76500:  -5.96671:  -7.99888:  -7.99674:   7.99783:  -4.08461:  -7.99972:  -7.99919:   7.99955:
   4(3): Nerr= 6, Ferr=   1.000, S=   1.065: :  -2.45119:  -7.99953:   7.99866:   2.75024:  -1.50152:  -7.99977:   5.16314:   3.76863:   0.30934:   7.99981:  -5.77530:  -7.99836:  -5.83957:  -2.83876:   5.73191:  -7.99954:  -7.99892:   7.99713:
   4(3): Nerr= 6, Ferr=   1.000, S=   1.065:
NeiroNetU, Ninput =2, Noutput=3, Nneirons=4, Nw=18, NteachPoins=25
Stype=3, fAct=2, Nerr=   6, Ferr=   1.00000, S= 1.0651471
       x[ 1] - input value (x-coord in plane)
       x[ 2] - input value (y-coord in plane)
       x[ 3] = f(  -2.451191   -7.999532*x[ 1]  +7.998663*x[ 2])
y[0] = x[ 4] = f(  +2.750240   -1.501521*x[ 1]  -7.999769*x[ 2]  +5.163142*x[ 3])
y[1] = x[ 5] = f(  +3.768634   +0.309341*x[ 1]  +7.999814*x[ 2]  -5.775300*x[ 3]  -7.998360*x[ 4])
y[2] = x[ 6] = f(  -5.839566   -2.838765*x[ 1]  +5.731905*x[ 2]  -7.999539*x[ 3]  -7.998924*x[ 4]  +7.997134*x[ 5])
--------------------------
   5(3): Nerr= 4, Ferr=   0.433, S=   1.063: :   0.93394:   7.99829:  -6.14492:   7.12364:  -3.20640:  -7.99969:  -3.61620:   7.99931:   3.33985:  -5.31981:  -7.99999:  -7.65292:  -4.94671:  -2.76427:   7.99912:   7.99636:  -7.99903:  -7.99927:
   5(3): Nerr= 4, Ferr=   0.433, S=   1.063:
NeiroNetU, Ninput =2, Noutput=3, Nneirons=4, Nw=18, NteachPoins=25
Stype=3, fAct=2, Nerr=   4, Ferr=   0.43333, S= 1.0629041
       x[ 1] - input value (x-coord in plane)
       x[ 2] - input value (y-coord in plane)
       x[ 3] = f(  +0.933943   +7.998286*x[ 1]  -6.144919*x[ 2])
y[0] = x[ 4] = f(  +7.123642   -3.206405*x[ 1]  -7.999689*x[ 2]  -3.616197*x[ 3])
y[1] = x[ 5] = f(  +7.999310   +3.339845*x[ 1]  -5.319814*x[ 2]  -7.999989*x[ 3]  -7.652917*x[ 4])
y[2] = x[ 6] = f(  -4.946711   -2.764270*x[ 1]  +7.999119*x[ 2]  +7.996358*x[ 3]  -7.999028*x[ 4]  -7.999273*x[ 5])
--------------------------
   6(3): Nerr= 7, Ferr=   1.100, S=   1.080: :  -2.63123:   5.31400:  -7.99920:   4.25314:  -7.99978:  -4.69914:   6.91804:   1.87055:   7.99968:   3.81567:  -5.94176:  -7.99970:  -7.99635:   7.99949:  -4.08617:  -7.99885:  -7.99883:   7.99834:
   7(3): Nerr= 6, Ferr=   1.000, S=   1.065: :  -2.45327:  -7.99822:   7.99963:   2.77559:  -1.53951:  -7.99995:   5.13772:   3.82698:   0.22289:   7.99944:  -5.83912:  -7.99914:  -5.82895:  -2.85391:   5.72687:  -7.99949:  -7.99945:   7.99667:
   8(3): Nerr=11, Ferr=   1.233, S=   1.261: :   7.16832:  -2.74793:  -7.99991:   3.90972:  -4.95484:  -7.99871:   7.99985:  -1.11980:  -7.99868:   5.47330:   7.99937:   7.99970:   7.99720:   7.99994:  -7.50316:  -7.41569:  -7.99879:  -7.99857:
   9(3): Nerr= 6, Ferr=   0.722, S=   1.144: :   7.49501:  -6.18796:  -7.99929:   4.21854:  -7.99961:  -7.99881:   7.99965:  -1.50729:  -7.99990:   7.36755:   3.29606:  -7.99967:  -4.13571:   3.87438:   7.99995:  -7.99862:   4.73640:  -7.99926:
  10(3): Nerr= 6, Ferr=   0.656, S=   1.103: :  -5.19642:   7.99879:  -4.48039:   5.59981:  -7.99930:  -6.18364:   3.82631:   0.61124:  -7.99936:   5.29179:  -7.99898:  -7.99965:   0.38138:   2.90705:   3.17484:  -7.99906:  -7.99983:  -7.99972:
  11(3): Nerr= 9, Ferr=   1.311, S=   1.180: :  -4.51052:   3.37878:   7.99980:   7.99926:  -3.45747:  -6.48183:  -7.99983:  -1.67375:   5.71299:   7.99972:   7.99935:  -7.99940:  -7.99947:   7.99927:  -7.14968:   7.99766:  -7.99985:   2.85194:
...

Для каждой попытки выводится Nerr - количество ошибок, Ferr - взвешенное количество ошибок, (вес редких кластеров больше), S - минимизируемая функция ошибок и вектор w внутренних параметров нашей нейронной сети.

Будем называть шаг удачным, если количество ошибок уменьшилось, или при том же количестве ошибок уменьшилась величина S. Для каждого удачного шага дополнительно те же коэффициенты записываются в виде формул, описывающих работу сети.

В нашем примере из 1757 шагов удачными оказались пять: 1, 4, 5, 19 и 123. Их результаты:

   1(3): Nerr= 6, Ferr=   1.000, S=   1.067: :   2.44947:   7.99755:  -7.99935:   7.94675:  -1.56349:  -7.99980:  -5.13109:  -1.94881:   0.37456:   7.99841:   5.78624:  -7.99911:  -7.99896:  -3.12359:   5.89210:   7.99990:  -7.99937:   2.17186:
   4(3): Nerr= 6, Ferr=   1.000, S=   1.065: :  -2.45119:  -7.99953:   7.99866:   2.75024:  -1.50152:  -7.99977:   5.16314:   3.76863:   0.30934:   7.99981:  -5.77530:  -7.99836:  -5.83957:  -2.83876:   5.73191:  -7.99954:  -7.99892:   7.99713:
   5(3): Nerr= 4, Ferr=   0.433, S=   1.063: :   0.93394:   7.99829:  -6.14492:   7.12364:  -3.20640:  -7.99969:  -3.61620:   7.99931:   3.33985:  -5.31981:  -7.99999:  -7.65292:  -4.94671:  -2.76427:   7.99912:   7.99636:  -7.99903:  -7.99927:
  19(3): Nerr= 4, Ferr=   0.433, S=   1.026: :  -3.26068:   7.99886:  -7.99968:   7.18514:  -7.99997:  -7.99900:   0.81236:   3.04033:  -7.99902:   2.33341:   7.99959:  -7.99986:   3.11496:   7.99992:  -3.38485:  -7.99873:  -7.99876:  -7.99985:
 123(3): Nerr= 3, Ferr=   0.322, S=   1.058: :  -1.50940:  -7.99999:   6.90892:   3.48089:  -3.06803:  -7.99997:   3.74948:   2.15881:   2.04043:  -6.98245:   7.99978:  -7.99889:   3.60328:  -3.08219:   7.99893:  -7.99923:  -7.99989:  -7.99848:

Многие значния близки к 8, но ...

В файлах Y_*.bmp лежат графические представления полученной кластеризации на каждом из удачных шагов:

Y_00001.bmp

Y_00004.bmp

Y_00005.bmp

Y_00019.bmp

Y_00123.bmp

В файлах N_02_*.bmp лежат графические представления значений нейронов на последнем удачном шаге, включая "виртуальные" нейроны N_02_0001.bmp N_02_0002.bmp представляющие x- и y-координаты входных данных.

N_02_0001.bmp

N_02_0002.bmp

N_02_0003.bmp

N_02_0004.bmp

N_02_0005.bmp

N_02_0006.bmp

В файле teach.png лежит графические представления исходных данных из матрицы matrix5.txt

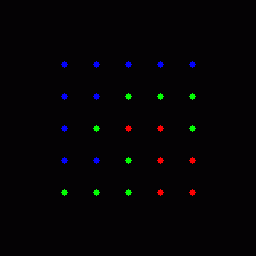teach.png