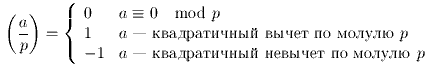
|
Пусть n – нечетное натуральное число, не являющееся полным квадратом. Обозначим через c наименьшее среди чисел [-1,2,3,5,7,11,...] такое, что символ Якоби jacobi(c/n) =-1. Если c ≤ 2, то положим z=2+sqrt(c), иначе z=1+sqrt(c). Назовем число n простым по Фробениусу, если Неизвестно ни одного числа, на котором метод ошибается. Доказано, что ошибок нет при n < 260. Фактически, метод объединяет методы Ферма и Lucas-Lemer'a. |
Простых чисел удивительно много. В таблице показана вероятность (в процентах) оказаться простым для k-значных чисел:
| Разрядность: | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 |
| Вероятность (%): | 20 | 14 | 10.8 | 8.67 | 7.23 | 6.20 | 5.43 | 4.83 | 4.34 | 3.62 | 2.90 | 2.17 |
Для сравнения, доля чисел, не имеющих делителей меньших 10k (в процентах):
| k: | 1 | 2 | 3 | 4 | 5 |
| Доля (%): | 22.86 | 12.03 | 8.10 | 6.09 | 4.88 |
Таким образом, если брать числа порядка нескольких миллиардов, не имеющих делителей меньше 1000, то примерно половина таких чисел будет простой. Среди 18-значных чисел не имеющих делителей меньше 1000 более трети просты.
Важной задачей до сих пор остается разработка эффективных методов проверки простоты. Даже самый простейший из них – метод последовательного деления на все простые числа не так плох. Для проверки простоты числа n достаточно проверить делимость на все простые числа, меньшие квадратного корня из n. Так как простых чисел, меньших 232 всего 203 280 221 штуки, то для проверки простоты числа < 264 требуется не более 200 млн. делений, то есть меньше секунды времени.
В современной критографии имеют практическое значение простые числа величиной до 21024 (~308 десятичных цифр), максимально до 23000 (~900 десятичных цифр). Таким образом, с практической точки зрения нам надо уметь проверять простоту чисел длиной до 1000 десятичных знаков. Для этого требуются уже другие методы.
Функция π(x)
Количество простых чисел, не превышающих x в теории чисел принято обозначать π(x). Приведем некоторые значения этой функции (подробнее, см.Computational projects):
| π(103) | π(106) | π(109) | π(232) | π(1012) | π(1015) | π(1018) | π(264) |
|---|---|---|---|---|---|---|---|
| 168 | 78 498 | 50 847 534 | 203 280 221 | 37 607 912 018 | 29 844 570 422 669 | 24 739 954 287 740 860 | 425 656 284 035 217 743 |
Разработано множество самых разнообразных алгоритмов таких проверок, см. например в Википедии . Большинство из них дают лишь вероятностный ответ: число может оказаться гарантировано составным, или «вероятно простым». То есть каждый из этих методов может принять некоторое составное число за простое, но не наоборот. Такие числа называются «псевдопростыми». Наиболее простой метод основан на малой теореме Ферма.
Теорема 1. Если p – простое и a не делится на p, то ap -1 ≡ 1 mod p.
Обратное утверждение неверно, то есть из того, что ap -1 ≡ 1 mod p не следует, что p – простое, например 211 · 31-1 ≡ 1 mod 11 · 31. Тем не менее, если для некоторого a выполнено an-1 ≡ 1 mod n, то число n почти наверняка простое.
Определение. Составное число n называется псевдопростым по основанию a, если an -1 ≡ 1 mod n.
Другими словами, пседопростые числа – это те, на которых предлженный метод проверки ошибается.
Псевдопростых чисел довольно много. Например, среди чисел меньших 232 псевдопростых по основанию 2 оказывается 10403 (на 200 млн. простых), среди чисел меньших 264 – 118 968 378 (на 4 · 1017 простых) (см. Jan Feitsma).
Проверка по нескольким различным основаниям сокращает количество ошибок, но не радикально. Например, среди 10403 чисел меньших 232 псевдопростых по основанию 2, псевдопростыми и по основанию 3 оказывается 2318 штук.
Интересно отметить, что псевдопростые числа могут иметь кратные множители. Однако такие числа должны иметь весьма специальный вид.
Теорема 2. Пусть n=pkq – псевдопросто по основанию a, где p – простое. Тогда p2, …, pk – псевдопросты по основанию a. Более того, в этом случае ap-1 ≡ 1 mod pk.
Простые числа p такие, что p2 псевдопросто по основанию a встречаются, но редко. Например, известно всего два таких числа при a=2. Это 1093 и 3511. Других таких чисел нет, по крайней мере при p < 758 · 109. Есть некоторые основания предполагать, что таких чисел больше нет вообще, но доказать это не удается.
Можно найти все такие пары (a,p), что ap-1 ≡ 1 mod p2 для a=2, … , 127 и p < 1010. Их оказалось 212:
a p a p a p a p 2 1093 25 53471161 62 1291 93 81551 2 3511 25 1645333507 63 36713 94 241 3 11 25 6692367337 63 401771 94 32143 3 1006003 26 71 64 1093 94 463033 4 1093 26 486999673 64 3511 95 2137 4 3511 26 6695256707 65 163 95 15061 5 20771 27 1006003 66 89351671 96 109 5 40487 30 160541 67 268573 96 5437 5 53471161 31 79 68 113 96 8329 5 1645333507 31 6451 68 2741 96 12925267 5 6692367337 31 2806861 69 223 97 2914393 6 66161 32 1093 69 631 98 28627 6 534851 32 3511 69 2503037 98 61001527 6 3152573 33 233 70 142963 100 487 7 491531 33 47441 71 331 100 56598313 8 1093 33 9639595369 75 347 101 1050139 8 3511 35 1613 75 31247 102 7559 9 11 35 3571 76 1109 102 11813 9 1006003 36 66161 76 9241 102 139409857 10 487 36 534851 76 661049 103 24490789 10 56598313 36 3152573 77 32687 104 313 11 71 37 77867 78 151 104 237977 12 2693 38 127 78 181 105 7669 12 123653 39 8039 78 1163 106 79399 13 863 40 307 78 56149 106 672799 13 1747591 40 66431 78 4229335793 107 613181 14 29 41 1025273 79 263 108 3761 14 353 41 138200401 79 3037 108 10271 14 7596952219 43 103 79 1012573 108 1296018233 15 29131 44 229 79 60312841 109 20252173 16 1093 44 5851 80 6343 110 5381 16 3511 45 1283 81 1006003 110 9431 17 46021 45 131759 83 4871 111 131 17 48947 45 157635607 83 13691 112 1037888513 18 37 46 829 83 315746063 114 9181 18 331 48 257 84 163 115 2743780307 18 33923 49 491531 84 653 117 182111 18 1284043 52 461 84 20101 118 3152249 19 43 52 1228488439 85 11779 118 10404887 19 137 53 59 86 68239 119 1741 19 63061489 53 97 86 6232426549 120 653 20 281 54 1949 87 1999 120 2074031 20 46457 55 30109 87 48121 120 124148023 20 9377747 55 7278001 88 2535619637 122 2791 20 122959073 56 647 90 6590291053 123 34849 22 673 56 7079771 91 293 124 22511 22 1595813 57 47699 92 727 125 20771 22 492366587 57 86197 92 383951 125 40487 23 2481757 58 131 92 12026117 125 53471161 23 13703077 58 42250279 92 18768727 125 1645333507 24 25633 59 2777 92 1485161969 125 6692367337 25 20771 60 9566295763 93 509 127 907 25 40487 62 127 93 9221 127 13778951
Можно проверить, что нет других пар вида (2, p) при p<758 · 109, вида (3, p) при p<681 · 109 и вида (5, p) при p<40 · 109.
Наименьшее число a, при котором не существует указанных пар (a,p) при p<5 · 1010 – это 21. Конечно, вряд ли стоит ожидать, что таких пар нет ни для каких p, скорее всего, это лишь вопрос объема вычислений. Тем не менее, нет и никаких оснований считать, что такие пары существуют для всех a.
С другой стороны, для каждого простого p существует достаточно много подходящих a, правда они равномерно расположены на большом отрезке 0 … p2.
Более подробно об этом можно прочитать здесь (pdf).
При рассмотрении чуть более сложных методов уже никак не обойтись без этих понятий. Поэтому рассмотрим их вкратце. Для более детального рассмотрения можно обратиться, например к Википедии или к литературе там приведенной.
Любое положительное действительное число является квадратом некоторого другого числа (и даже двух): 25 является квадратом 5 и -5, число 7 является квадратом sqrt(7) и -sqrt(7). Отрицательные числа не являются ни чьими квадратами, ноль является квадратом только самого себя.
Для вычетов по простому модулю ситуация вполне аналогичная. Пусть p – простое число, для примера возьмем p=11. Рассмотрим квадраты всех ненулевых вычетов по модулю p:
| x : | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x2: | 1 | 4 | 9 | 5 | 3 | 3 | 5 | 9 | 4 | 1 |
Определение. Для простого p и целого a определим символ Лежандра следующим образом:
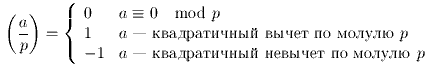
Мультипликативность.
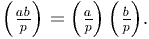
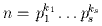
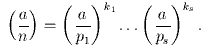
Квадратичный закон взаимности. Пусть p,q - нечётные числа. Тогда
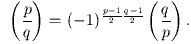
Частные случаи.
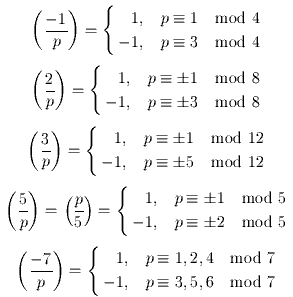
x2 ≡ ap-1 ≡ 1 mod p,
поэтому x ≡ ±1 mod p. На самом деле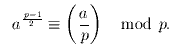
Проверка этого соотношения для данного числа n и называется тестом Соловея-Штрассена («СШ(a)»).
На 203 миллиона простых, меньших 232 псевдопростых по основанию 2 всего 10403, из них тест Соловея-Штрассена проходят 5367 чисел.
Другим усилением метода Ферма является «метод Миллера-Рабина» .
Пусть p — простое и p-1 делится на 2k, p-1 = q•2k. Обозначим aq через y. Согласно теореме Ферма,
Пусть, например k=4. Тогда y 16 -1 ≡ 0 mod p или
Так как кольцо вычетов по простому модулю является полем и, следовательно, не имеет делителей нуля, одна из этих скобок должна равняться 0. Эта проверка для данного числа n и называется тестом Миллера-Рабина («МР(a)»).
Тест Миллера-Рабина более сильный (включает в себя) чем тест Соловея-Штрассена.
Составные числа, проходящие тест Миллера-Рабина по основанию a называются сильно псевдопростыми числами (strong pseudoprimes, SPSP(a)).
Среди чисел меньших 232 :
| простых: | 203 280 221 |
| псевдопростых по основанию 2: | 10403 |
| «СШ(2)» | 5367 |
| «МР(2)» | 2314 |
| псевдопростых по основаниям 2 и 3: | 2318 |
| «СШ(2)» и «СШ(3)» | 969 |
| «МР(2)» и «МР(3)» | 104 |
| «МР(2)», «МР(3)» и «МР(5)» | 6 |
1373653 1530787 1987021 2284453 3116107
5173601 6787327 11541307 13694761 15978007
16070429 16879501 25326001 27509653 27664033
28527049 54029741 61832377 66096253 74927161
80375707 101649241 102690677 104852881 105919633
106485121 117987841 143168581 154287451 161304001
193949641 206304961 218642029 223625851 247318957
252853921 259765747 275619961 314184487 326695141
390612221 393611653 489994201 540654409 572228929
579606301 581618143 682528687 717653129 745745461
787085857 846961321 871157233 927106561 938376181
960946321 979363153 981484561 1028494429 1157839381
1168256953 1236313501 1463178817 1481626513 1518290707
1521221473 1538012449 1638294661 1854940231 1856689453
1860373241 1909566073 1921309633 1991063449 1995830761
2057835781 2117555641 2217879901 2284660351 2311558021
2323147201 2412172153 2431144801 2626783921 2693739751
2736316301 2781117721 2837917633 3028586471 3056100623
3215031751 3299246833 3344191241 3407772817 3513604657
3697278427 3708905341 3863326897 3867183937 4060942381
4079665633 4117447441 4275011401 4277526901
На самом деле, для проверки на простоту чисел меньших 4 759 123 141
достаточно выполнить тесты МР(2), МР(7) и МР(61)
(см.
здесь).
Прямая проверка показывает, что
В тоже время, существуют методы, которые, хотя и дают довольно много ошибок, но на совершенно других числах, чем методы, основанные на теореме Ферма. Один из них – «метод Люка» (он же - «Люк-Лемер»). Некоторый вариант его совместного применения с методом Ферма называется BPSW-методом.
Определение. Пусть P,Q – два целых числа. Последовательностями Люка Un=Un(P,Q) и Vn=Vn(P,Q) называются последовательности, удовлетворяющие рекуррентному соотношению
при n ≥ 2 и начальным условиям
При P=1 и Q= -1 получаем:
При P=2 и Q= -1:
При P=3 и Q= 2:
Число D=P2-4Q называется дискриминантом последовательности. В содержательных случаях оно не должно быть полным квадратом. Для чисел Фибоначчи дискриминант равен 5.
Теорема 3. Пусть
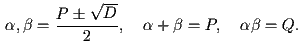
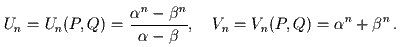
Последовательности Люка имеют множество интересных свойств. Все они довольно легко
выводятся из этой формулы. Подробнее можно прочитать в книге
Paulo Ribenboim. My Numbers, My Friends. Popular Lectures on Number Theory (.pdf).
Алгоритмы проверки простоты числа связанные с числами Люка основаны на том,
что если p - простое
и символ Якоби jacobi(D, p)=-1, то иррациональная часть числа αk
равна 0, если k делится на p+1. Если же число n не простое,
то иррациональная часть числа αn+1 тоже может оказаться равна 0, но
очень редко. Подробнее см., например,
Crandall R. Pomerance C. Prime Numbers: A Computational Perspective.
или в Википедии:
Псевдопростое число Люка.
Основное достоинство такого метода проверки состоит в том, что он ошибается совсем на других числах, чем методы, основанные на теореме Ферма. Поэтому совместное применение методов Миллера-Рабина и Люка дает очень надежный результат.
На сегодняшний день нет ни одного примера, когда бы эти методы одновременно ошиблись!
Для работы с целыми числами произвольного размера в языке Java имеется класс BigInteger. Среди методов этого класса, помимо стандартных арифметических операций, выделим следующие:
Так как все стандартные библиотеки языка Java поставляются вместе с исходными текстами, их реализацию можно подробно изучить (src.zip\java\math\BigInteger.java). Для работы с классом BigInteger не требуется никаких дополнительных библиотек, что так же является существенным фактором.
Приведем время выполнения ключевой операции modPow, на процессоре Intel i5 с тактовой частотой 2.27 ГГц (Win-64) в зависимости от разрядности чисел:
| Длина, бит | Время, мс |
|---|---|
| 64 | 0.008 |
| 128 | 0.034 |
| 256 | 0.14 |
| 512 | 0.75 |
| 1024 | 4.7 |
| 2048 | 35 |
Для вероятностной проверки чисел на простоту в языке Java служит метод класса BigInteger
public boolean isProbablePrime(int certainty);
Он работает следующим образом. Если проверяемое число имеет длину не больше 100 битов, то выполняется certainty/2 (но не более 50) тестов Миллера-Рабина по случайному основанию a.
Если число имеет длину больше 100 битов, то проверка выполняется в два шага. На первом опять же выполняется certainty/2 тестов Миллера-Рабина по случайному основанию a, но их предельное количество зависит от длины числа в битах:
if (sizeInBits < 256) rounds = 27;
else if (sizeInBits < 512) rounds = 15;
else if (sizeInBits < 768) rounds = 8;
else if (sizeInBits < 1024)rounds = 4;
else rounds = 2;
После этих проверок, на втором шаге выполняется ещё и проверка методом Люка-Лемера :
private boolean passesLucasLehmer();
Экспериментальный факт. В языке Java невозможно получить ошибку в методе isProbablePrime класса BigInteger для чисел длиннее 100 битов ни при каком уровне надежности большем 0.
И это неспроста, см. ниже, метод Фробениуса.
Определение. Квадратичной иррациональностью будем называть число вида z=a+b sqrt(c), где a,b,c – целые числа, причем c свободно от квадратов.
Через z mod n будем обозначать число (a mod n)+(b mod n) sqrt(c).
Сопряженным числом будем называть число z=a-b sqrt(c).
Сопряжение мультиптикативно:
Норма мультиптикативна:
и
N(z) =N( z) = -2,
z11 = 31648+18272 sqrt(3)
N(z11) = -2048 = (-2)11,
Вычисление za mod n примерно вдвое сложнее, чем таже операция для целых чисел.
Теорема 4. Если символ Якоби jacobi(c,p) равен -1, то квадратичные иррациональности по простому модулю p образуют поле (поле Галуа) из p² элементов, обозначаемое Zp[sqrt(c)].
Теорема 5 (Фробениуса). Пусть p - простое, jacobi(c,p)=-1 и z принадлежит Zp[sqrt(c)]. Тогда
|
Пусть n – нечетное натуральное число, не являющееся полным квадратом. Обозначим через c наименьшее среди чисел [-1,2,3,5,7,11,...] такое, что символ Якоби jacobi(c/n) =-1. Если c ≤ 2, то положим z=2+sqrt(c), иначе z=1+sqrt(c). Определение. Назовем число n простым по Фробениусу, если Фактически, метод объединяет методы Ферма и Lucas-Lemer'a. Неизвестно ни одного числа, псевдопростого по Фробениусу, т.е. на котором метод ошибается. Доказано, что таких чисел нет меньших < 260. Кратный простой множитель FPP-числа не может быть меньше 232. Простой множитель p FPP-числа n, у которого jacobi(c/p)=1, не может быть меньше 232. Пусть p - простой множитель FPP-числа n, тогда n/p > 218. |
Замечание. Термин "тест Фробениуса" (проверки простоты чисел) иногда используется в несколько другом смысле, см., например,
Теорему Фробениуса можно использовать для простроения вероятностного теста простоты числа.
Пусть n > 1 - нечётное, числа a,b,c таковы, что a, b, c взаимно просты с n, a²-b²c ≠ 0,1 mod n и jacobi(c/n)=-1. Тогда, если
Как и в других аналогичных тестах для повышения надежности можно было бы потребовать выполнить этот тест несколько раз с различными a,b (менять c нет смысла). Но это излишне.
На сегодняшний день не известно НИ ОДНОГО контрпримера к этому тесту!
Доказано, что их нет при n < 260.
Замечание. В книге
Richard Crandall; Carl Pomerance (2005). Prime numbers: A computational perspective (2nd ed.). Springer-Verlag. ISBN 0-387-25282-7
на стр. 146 контрпримеры приводятся. Однако тест Фробениуса в этом месте книги
понимается в несколько другом смысле.
Учитывая отсутствие контрпримеров, вместо того, чтобы говорить о произвольном (случайном) выборе параметров a, b, c, мы их просто зафиксируем.
Определение. Пусть n – нечетное натуральное число, не являющееся полным квадратом. Его индексом Фробениуса IndF(n) будем называть наименьшее среди чисел [–1,2,3,4,5,6,...] такое, что символ Якоби jacobi(c/n) =–1.
Из мультипликативности символа Якоби следует, что если индекс c = IndF(n) положителен, то он прост.
Нетрудно выяснить, когда индекс Фробениуса принимает маленькие значения:
Определение.
Пусть n – нечетное натуральное число, не являющееся полным квадратом,
обозначим IndF(n) через c.
Если c ≤ 2, то положим z=2+sqrt(c), иначе z=1+sqrt(c).
Назовем число n простым по Фробениусу, если
Пример 1. Пусть n=19. Тогда c=-1, z=2+i,
Пример 2. Пусть n=33. Тогда c=-1, z=2+i,
Пример 3. Пусть n=17. Тогда c=3, z=1+sqrt(3),
Конечно, нас интересуют случаи, когда этот метод ошибается.
Определение. Составное нечетное натуральное число n назовем псевпопростым по Фробениусу (Frobenius pseudoprime, FPP), если оно просто по Фробениусу.
Отметим, что если n псевдопросто по Фробениусу, то n псевдопросто по основанию N(z), то есть тест Фробениуса включает в себя тест Ферма.
Гипотеза. Псевдопростых по Фробениусу чисел не существует!
Другими словами, тест Фробениуса никогда не ошибается.
Не надо пытаться найти контрпример прямым перебором. Доказано, что его нет среди чисел меньших 260. Гораздо больше шансов найти его в виде произведения простых.
Для числа n, псевдопростого по Фробениусу, зафиксируем обозначения:
В определении простоты по Фробениусу входит нахождение индекса Фробениуса. Насколько он может быть велик? Да насколько угодно. Однако, если рассматривать числа ограниченной длины, то можно найти и ограничение для этого индекса. Доказано, что если брать числа, меньшие 264, то их индекс Фробениуса не превышает 277. Более того, чисел с индексом больше 128 имеется 458 069 912 штук и все они не являются псевдопростыми.
Таким образом проверено, что для псевдопросых по Фробениусу чисел меньших 264,
их индекс Фробениуса не превышает 127.
Ф-положительные делители
Определение. Пусть n псевдопросто по Фробениусу, c = IndF(n) - его индекс Фробениуса. Простой делитель p числа n будем называть Ф-отрицательным, если символ Якоби jacobi(c/p)=-1 и Ф-положительным, если jacobi(c/p)=1.
Напомню, что согласно определению, если jacobi(c/p)=1, то
c является квадратом по простому модулю p, то есть существует d
такое, что c ≡ d 2 mod p.
Ф-положительные делители у псевдопростых по Фробениусу чисел должны удовлетворять
некоторому условию, которое выполняется очень редко. Подробности
здесь.
Кратные множители
Теорема. Пусть n псевдопросто по Фробениусу и n = psq, где p - Ф-отрицательный множитель и s > 1. Тогда
Простые числа, удовлетворяющие этому условию встречаются редко, не удалось найти ни одного примера таких чисел. Прямым перебором можно получить следующее.
Предложение. У псевдопростых по Фробениусу чисел при c < 128 не существует не существует кратных множителей меньших 232.