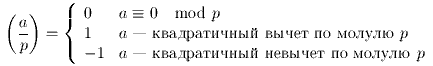
Проверка чисел на простоту. Метод Фробениуса.
Определение. Для простого p и целого a определим символ Лежандра следующим образом:
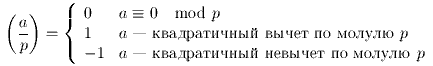
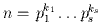
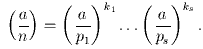
Квадратичный закон взаимности. Пусть p,q - нечётные числа. Тогда
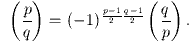
Частные случаи.
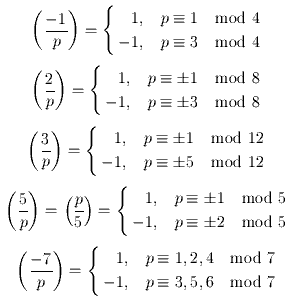
Нам потребуется похожее, но чуть другое понятие, "наименьший по абсолютной величине квадратичный невычет".
Определение. Пусть n – нечетное натуральное число, не являющееся полным квадратом. Его индексом Фробениуса IndF(n) будем называть наименьшее среди чисел [–1,2,3,4,5,6,...] такое, что символ Якоби jacobi(c/n) =–1.
Замечание 1. Из мультипликативности символа Якоби следует, что если индекс Фробениуса IndF(n) положителен, то он прост.
Замечание 2. Если jacobi(-1/n) =+1, то jacobi(-c/n) = jacobi(c/n) для всех c.
Нетрудно выяснить, когда индекс Фробениуса принимает маленькие значения:
jacobi(c/n) = jacobi(n/c)
то есть символ Якоби jacobi(c/n) зависит только от n mod c.Таким образом, индекс Фробениуса для большинтва чисел невелик, -1,2,3,5. Однако, для некоторых чисел он может оказаться довольно большим:
| n | Разложение | IndF(n) |
|---|---|---|
| 73 | 73 | 5 |
| 241 | 241 | 7 |
| 1 009 | 1009 | 11 |
| 2 641 | 19*139 | 13 |
| 8 089 | 8089 | 17 |
| 18 001 | 47*383 | 19 |
| 53 881 | 53 881 | 23 |
| 87 481 | 87481 | 29 |
| 117 049 | 67*1747 | 31 |
| 515 761 | 515 761 | 37 |
| 1 083 289 | 1083 289 | 41 |
| 3 206 641 | 643*4987 | 43 |
| 3 818 929 | 3818 929 | 47 |
| 9 257 329 | 9257 329 | 53 |
| 22 000 801 | 22 000 801 | 59 |
| 56 588 401 | 67*844 603 | 61 |
| 48 473 881 | 48 473 881 | 67 |
| 175 244 281 | 175 244 281 | 71 |
| 872 479 969 | 577*1512 097 | 73 |
| 427 733 329 | 427 733 329 | 79 |
| 898 716 289 | 898716289 | 83 |
| 4 210 182 001 | 277*15 199 213 | 89 |
| 9 176 747 449 | 9176747449 | 97 |
| 2 805 544 681 | 127*859*25717 | 101 |
| 10 310 263 441 | 4007*2 573 063 | 103 |
| 23 616 331 489 | 23 616 331 489 | 107 |
Для чисел, меньших 264 наибольший индекс Фробениуса имеют числа
13 371 308 337 168 834 529 = 15671 * 42 509 111 * 20 072 209, и
10 198 100 582 046 287 689 = 277 * 1091 * 1151 * 29 318 344 777,
Их индекс Фробениуса равен 277.
Приведем полный список чисел, меньших 264 с индексом Фробениуса ≥ 241:
| n | Разложение | IndF(n) |
|---|---|---|
| 10 198 100 582 046 287 689 | 277 * 1091 * 1151 * 29318344777 | 277 |
| 13 371 308 337 168 834 529 | 42509111 * 20072209 * 15671 | 277 |
| 14 556 961 869 213 641 641 | 294859 * 49369230273499 | 269 |
| 8 019 204 661 305 419 761 | 85049496359 * 15329 * 6151 | 263 |
| 15 559 176 909 429 792 409 | 15559176909429792409 | 257 |
| 9 525 254 728 650 901 321 | 269356523164067 * 35363 | 257 |
| 6 384 991 873 059 836 689 | 56634160359229 * 112741 | 257 |
| 15 841 063 060 186 483 729 | 15841063060186483729 | 257 |
| 15 615 860 448 589 902 601 | 269 * 449 * 20918629 * 6180649 | 251 |
| 15 161 588 123 783 204 041 | 15161588123783204041 | 251 |
| 15 092 828 713 838 767 369 | 487 * 87168671 * 9221 * 38557 | 251 |
| 12 144 088 165 752 308 089 | 1034549 * 283176937 * 41453 | 251 |
| 10 918 467 669 293 400 241 | 569 * 360603871 * 53213159 | 251 |
| 9 064 125 655 411 231 729 | 9064125655411231729 | 251 |
| 8 296 704 369 880 085 329 | 224719730759 * 36920231 | 251 |
| 7 709 526 364 683 482 161 | 2513702759922883 * 3067 | 251 |
| 4 874 863 023 350 911 369 | 3292229887 * 1480717687 | 251 |
| 2 327 687 064 124 474 441 | 479 * 4859471950155479 | 251 |
| 18 229 083 490 490 001 529 | 18229083490490001529 | 241 |
| 18 160 759 655 635 441 441 | 728788153 * 6188011 * 4027 | 241 |
| 17 895 360 545 240 844 241 | 17895360545240844241 | 241 |
| 17 730 965 717 070 847 609 | 17730965717070847609 | 241 |
| 16 539 844 297 164 123 961 | 821 * 3421242053 * 5888497 | 241 |
| 16 051 125 467 279 775 889 | 41255129 * 11128681 * 34961 | 241 |
| 15 563 774 009 731 253 329 | 5238710509 * 4597 * 646273 | 241 |
| 15 500 304 528 660 177 769 | 773 * 20052140399301653 | 241 |
| 14 579 447 188 898 695 321 | 14579447188898695321 | 241 |
| 14 076 396 959 102 325 961 | 14076396959102325961 | 241 |
| 14 062 107 862 023 021 529 | 1470583982389 * 9562261 | 241 |
| 13 962 703 804 646 805 289 | 313 * 641 * 647 * 564407 * 190577 | 241 |
| 13 270 764 547 337 857 921 | 463 * 1216294843 * 23565469 | 241 |
| 13 194 818 078 923 010 209 | 1607359980378001 * 8209 | 241 |
| 13 152 535 378 957 253 449 | 1358873373174631 * 9679 | 241 |
| 12 780 228 604 848 907 801 | 251 * 50917245437645051 | 241 |
| 12 198 313 032 091 127 881 | 528089480431 * 23098951 | 241 |
| 12 139 477 918 848 888 721 | 12139477918848888721 | 241 |
| 11 631 303 398 465 948 521 | 540462961687001 * 21521 | 241 |
| 11 417 898 363 696 440 641 | 1823071748953607 * 6263 | 241 |
| 11 257 547 117 859 426 409 | 941 * 971 * 12320686866919 | 241 |
| 11 142 142 214 574 728 569 | 281 * 39651751653290849 | 241 |
| 10 806 857 647 730 657 041 | 108327479152481 * 99761 | 241 |
| 10 565 328 852 664 066 849 | 10565328852664066849 | 241 |
| 10 096 447 955 180 345 641 | 10096447955180345641 | 241 |
| 6 938 117 179 828 687 609 | 6938117179828687609 | 241 |
| 5 799 375 985 159 604 761 | 166923876599 * 34742639 | 241 |
| 4 850 624 987 082 642 769 | 599 * 1163 * 4045854797 * 1721 | 241 |
| 1 773 855 791 877 850 321 | 4977618781 * 356366341 | 241 |
Количество чисел, меньших 264 с данным индексом Фробениуса таково
| IndF | Количество |
|---|---|
| 277 | 2 |
| 271 | 0 |
| 269 | 1 |
| 263 | 1 |
| 257 | 4 |
| 251 | 10 |
| 241 | 29 |
| 239 | 61 |
| 233 | 136 |
| 229 | 306 |
| 227 | 704 |
| 223 | 1 569 |
| 211 | 3 353 |
| 199 | 7 578 |
| 197 | 16 382 |
| 193 | 35 460 |
| 191 | 76 144 |
| 181 | 160 500 |
| 179 | 340 954 |
| 173 | 717 462 |
| 167 | 1 502 782 |
| 163 | 3 133 342 |
| 157 | 6 507 483 |
| 151 | 13 454 113 |
| 149 | 27 707 022 |
| 139 | 56 908 219 |
| 137 | 116 444 144 |
| 131 | 237 733 823 |
Всего среди чисел, меньших 264 индекс Фробениуса больший 128 имеют 458 069 912 чисел. Это количество велико, однако все эти числа вполне можно перебрать на современных (2015) компьютерах за приемлемое время.
Как же найти все такие числа? Очевидно, полный перебор слишком велик, даже если рассматривать только числа сравнимые с 1 по модулю 24.
Сформулируем ещё раз задачу.
Требуется найти все нечётные натуральные числа n < 264 не являющиеся полными квадратами такие, что символы Якоби
jacobi(-1/n)= jacobi(2/n)= jacobi(3/n)= ... = jacobi(127/n)=+1.
Числа, для которых
jacobi(-1/n)= jacobi(2/n)= jacobi(3/n)= +1
это в точности числа, сравнимые с 1 по модулю 24. Таким образом, надо найти числа n ≡ 1 mod 24, меньшие 264 такие, что
jacobi(5/n)= jacobi(7/n)= jacobi(11/n)= ... = jacobi(127/n)=+1.
Обозначим через
N=5 · 7 · ... · 47 = 102481630431415235
произведение 15-ти простых чисел, при этом 264 ≈ 7.5 · 24 · N.
Для каждого простого p=5,7,..., 47 обозначим через Xp множество вычетов t по модулю p таких, что
jacobi( 1 + 24 · N/p · t /p ) =1,
Множество Xp состоит из (p-1)/2 элементов. Выберем из каждого Xp по одному элементу xp. Тогда для числа
n = 1 + 24(N/5) x5 + ... + 24(N/47) x47
будет выполнено
jacobi(5/n)= jacobi(7/n)= ... = jacobi(47/n)=+1.
Чисел n такого вида будет(5-1)/2 * ... *(47-1)/2 = 5 205 549 888 000.
Это большое количество, однако их все можно перебрать даже на персональных компьютерах.Для каждого такого n рассматриваем все числа
n, n+24N, n+2 · 24N, ...
меньшие 264, их будет либо 7, либо 8 в зависимости от n. Для каждого такого числа надо проверить символы Якоби
jacobi(53/n), ..., jacobi(127/n)
и если все они равны 1 и n не является полным квадратом, то выводим такое число в выходной файл.
Отметим, что все n сравнимы с 1 по модулю 4, поэтому
jacobi(p/n) = jacobi(n/p) ,
поэтому вычисление символов Якоби можно свести к обращению к таблице, и выполнить достаточно быстро.
Результатом работы является текстовый файл, из 458 069 912 строк, в каждой лежит по одному числу, удовлетворяющему условиям
jacobi(-1/n)= jacobi(2/n)= jacobi(3/n)= ... = jacobi(127/n)=+1.
и не являющиеся полным квадратом.